Lớp 12 - Toán học - Nâng cao Giải bài 76, 77, 78, 79 trang 63, 64 SGK Giải tích 12 Nâng cao
Bài 76 trang 62 SGK giải tích 12 nâng cao
Cho hàm số \(f\left( x \right) = {x^4} - {x^2}\)
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số đã cho.
b) Từ đồ thị của hàm số y = f(x) suy ra cách vẽ đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\)
Giải
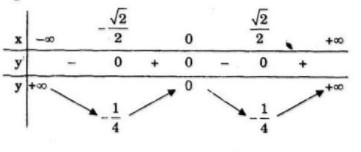
a) Tập xác định: \(D=\mathbb R\)
\(\eqalign{
& y' = 4{x^3} - 2x \cr
& y' = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = {{\sqrt 2 } \over 2} \hfill \cr
x = - {{\sqrt 2 } \over 2} \hfill \cr} \right. \cr} \)
Hàm số đồng biến trên khoảng: \(\left( { - {{\sqrt 2 } \over 2};0} \right)\) và \(\left( {{{\sqrt 2 } \over 2}; + \infty } \right)\)
Hàm số nghịch biến trên khoảng: \(\left( { - \infty ; - {{\sqrt 2 } \over 2}} \right)\) và \(\left( {0;{{\sqrt 2 } \over 2}} \right)\)
+) Cực trị:
Hàm số đạt cực đại tại: \(x=0;\;\;y(0)=0\)
Hàm số đạt cực tiểu tại: \(x={{\sqrt 2 } \over 2}\) và \(x=-{{\sqrt 2 } \over 2}\); \(y\left( { \pm {{\sqrt 2 } \over 2}} \right) = - {1 \over 4}\)
+) Giới hạn:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)
Bảng biến thiên:
Đồ thị:
Đồ thị cắt \(Ox\) và \(Oy\) tại \(O(0;0);(-1;0);(1;0)\)
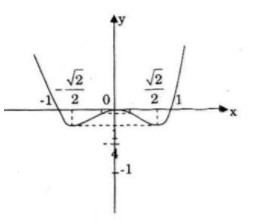
Đồ thị hàm số là hàm chẵn nên nhận trục Oy làm trục đối xứng.
b) Ta có
\(y = \left| {f\left( x \right)} \right| = \left\{ \matrix{
f\left( x \right)\,\,\,\text{nếu}\,\,\,f\left( x \right) \ge 0 \hfill \cr
- f\left( x \right)\,\,\,\text{nếu}\,\,\,f\left( x \right) < 0 \hfill \cr} \right.\)
Suy ra cách vẽ đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\)
Giữ nguyên phần đồ thị hàm số y = f(x) ở phía trên trục hoành. Lấy phần đồ thị hàm số ở phía dưới trục hoành đối xứng qua trục hoành. Hợp hai phần đồ thị trên ta được đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\)
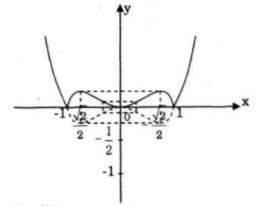
Bài 77 trang 62 SGK giải tích 12 nâng cao
Cho hàm số: \(y = {{x - 4m} \over {2\left( {mx - 1} \right)}}.\,\,\,\left( {{H_m}} \right)\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số với m =1.
b) Chứng minh rằng với mọi \(m \ne \pm {1 \over 2}\), các đường cong \(\left( {{H_m}} \right)\) đều đi qua hai điểm cố định A và B.
Giải
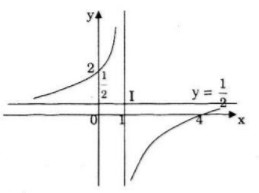
a) m=1 hàm số có dạng: \(y = {{x - 4} \over {2x - 2}}\)
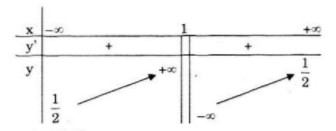
Tập xác định: \(D = R\backslash \left\{ 1 \right\}\)
\(y' = {6 \over {{{\left( {2x - 2} \right)}^2}}} > 0\,,\forall x \in D\)
Hàm số đồng biến trên khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\)
Hàm số không có cực trị
Giới hạn:
\(\mathop {\lim y}\limits_{x \to {1^ - }} = + \infty ;\mathop {\lim y}\limits_{x \to {1^ + }} = - \infty \)
Đường tiệm cận đứng: \(x=1\)
\(\mathop {\lim }\limits_{x \to \pm \infty } y = {1 \over 2}\)
Đường tiệm cận ngang \(y={1 \over 2}\)
Bảng biến thiên:
Đồ thị:
Đồ thị giao Ox, Oy tại các điểm: (4;0); (0;2)
b) Gọi \(M\left( {{x_o};{y_o}} \right)\) là một điểm bất kì của mặt phẳng tọa độ. Đường cong \(\left( {{H_m}} \right)\) đi qua điểm M khi và chỉ khi m là nghiệm của phương trình \({{{x_o} - 4m} \over {2\left( {m{x_o} - 1} \right)}} = {y_o}\)
\( \Leftrightarrow \left\{ \matrix{
m{x_o} - 1 \ne 0 \hfill \cr
2{y_o}\left( {m{x_o} - 1} \right) = {x_o} - 4m \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
m{x_o} \ne 1\,\,\,\,\,\,\left( 1 \right) \hfill \cr
\left( {2{x_o}{y_o} + 4} \right)m - {x_o} - 2{y_o} = 0\,\,\,\left( 2 \right) \hfill \cr} \right.\)
Mọi đường cong \(\left( {{H_m}} \right)\) với \(m \ne \pm {1 \over 2}\) đều đi qua điểm \(M\left( {{x_o};{y_o}} \right)\) khi và chỉ khi hệ phương trình trên nghiệm đúng với mọi \(m \ne \pm {1 \over 2}\).
Phương trình (2) nghiệm đúng với mọi m khi và chỉ khi
\(\left\{ \matrix{
2{x_o}{y_o} + 4 = 0 \hfill \cr
{x_o} + 2{y_o} = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_o} = - 2 \hfill \cr
{y_o} = 1 \hfill \cr} \right.\,\,\text{hoặc}\,\,\left\{ \matrix{
{x_o} = 2 \hfill \cr
{y_o} = - 1 \hfill \cr} \right.\)
Vậy \(\left( {{x_o};{y_o}} \right)\) =(-2;1) và \(\left( {{x_o};{y_o}} \right)\)=(2;-1)
Ta kiểm tra điều kiện (1)
• Với \({x_o} = - 2\), ta có \(m \ne - {1 \over 2}\)
•Với \({x_o} = 2\), ta có \(m \ne {1 \over 2}\)
Vậy mọi đường cong \(\left( {{H_m}} \right)\) với \(m \ne \pm {1 \over 2}\) đều đi qua hai điểm cố định A(-2; 1) và B(2; - 1).
c) Ta có \(y' = {{4{m^2} - 1} \over {2{{\left( {mx - 1} \right)}^2}}}\)
Hệ số góc tiếp tuyến với \(\left( {{H_m}} \right)\) tại A(-2; 1) và \(B(2; - 1)\) là y’(-2);y'(2).
Ta có tích hai hệ số góc tiếp tuyến tại A và B là:
\(y'\left( { - 2} \right).y'\left( 2 \right) = {{4{m^2} - 1} \over {2{{\left( {-2m - 1} \right)}^2}}}.{{4{m^2} - 1} \over {2{{\left( {2m - 1} \right)}^2}}} = {1 \over 4}\) là hằng số.
Bài 78 trang 62 SGK giải tích 12 nâng cao
a) Vẽ đồ thị (P) của hàm số \(y = {x^2} - x + 1\) và đồ thị (H) của hàm số \(y = {1 \over {x + 1}}\).
b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng.
c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).
Giải
a) Đồ thị
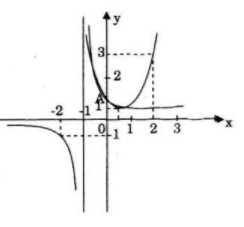
b) Hoành độ giao điể của parabol (P) và hypebol (H) là nghiệm của phương trình:
\({x^2} - x + 1 = {1 \over {x + 1}} \Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = 1\) (vì x = -1 không là nghiệm của phương trình)
\( \Leftrightarrow {x^3} + 1 = 1 \Leftrightarrow x = 0;\,\left( {y\left( 0 \right) = 1} \right)\)
Giao điểm của (P) và (H) là A(0;1)
Đặt \(f\left( x \right) = {x^2} - x + 1;\,g\left( x \right) = {1 \over {x + 1}}\)
Ta có: \(f'\left( x \right) = 2x - 1;\,g'\left( x \right) = - {1 \over {{{\left( {x + 1} \right)}^2}}}\)
\(f'\left( 0 \right) = g'\left( x \right) = - 1\)
Suy ra (P) và (H) có tiếp tuyến chung tại A nên (P) và (H) tiếp xúc nhau tại điểm A.
c) Xét hiệu \(f\left( x \right) - g\left( x \right) = {x^2} - x +1 - {1 \over {x + 1}} = {{{x^3}} \over {x + 1}}\)
Bảng xét dấu f(x) – g(x)
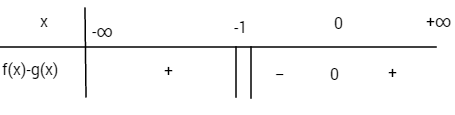
Trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0; + \infty } \right)\) (P) nằm phía trên (H). Trên khoảng \(\left( { - 1;0} \right)\) (P) nằm phía dưới (H).
Bài 79 trang 62 SGK giải tích 12 nâng cao
Cho hàm số : \(y = f\left( x \right) = x + {1 \over x}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b) Tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\) cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và tam giác OAB có diện tích không phụ thuộc vào vị trí điểm M trên đường cong (C).
Giải
a)
Tập xác định: \(D = R\backslash \left\{ 0 \right\}\)
\(\eqalign{
& y' = 1 - {1 \over {{x^2}}} = {{{x^2} - 1} \over {{x^2}}} \cr
& y' = 0 \Leftrightarrow x = \pm 1 \cr} \)
Hàm số đồng biến trên khoảng: \(\left( { - \infty ; - 1} \right)\left( {1; + \infty } \right)\)
Hàm số nghịch biến trên khoảng: \(\left( { - 1;0} \right)\left( {0;1} \right)\)
+) Cực trị:
Hàm số đạt cực đại tại: \(x=-1 ; y(-1)= -2\)
Hàm số đạt cực tiểu tại: \(x=1;y(1)=2\)
+) Giới hạn:
\(\mathop {\lim y}\limits_{x \to {0^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {0^ + }} = + \infty \)
Tiệm cận đứng: \(x=0\)
\(\mathop {\lim }\limits_{x \to \pm \infty } y = \pm \infty \)
\(\mathop {\lim }\limits_{x \to \infty } (y - x) = \mathop {\lim }\limits_{x \to \infty } {1 \over x} = 0\)
Tiệm cận xiên: \(y=x\)
Bảng biến thiên:
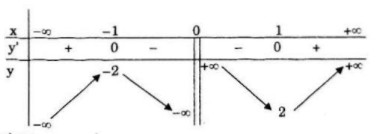
Đồ thị:
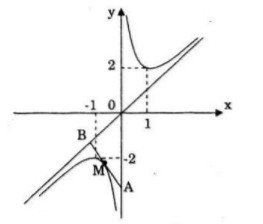
b) Tiệm cận đứng x = 0; Tiệm cận xiên y = x.
Ta có \(f\left( x \right) = 1 - {1 \over {{x^2}}}\). Phương trình tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\) là \(y = \left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}}\)
Thay x = 0 vào phương trình trên, ta được tung độ của điểm A:
\({y_A} = \left( {1 - {1 \over {x_o^2}}} \right)\left( { - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = {2 \over {{x_o}}}\). Vậy \(A\left( {0;{2 \over {{x_o}}}} \right)\)
Hoành độ của điểm B là nghiệm của phương trình
\(\left( {1 - {1 \over {x_o^2}}} \right)\left( {x - {x_o}} \right) + {x_o} + {1 \over {{x_o}}} = x \)
\(\Leftrightarrow - {x \over {{x_o}}} + {2 \over {{x_o}}} = 0 \Leftrightarrow x = 2{x_o}\)
\({x_B} = 2{x_o}\). Vậy \(B\left( {2{x_o};2{x_o}} \right)\)
Ta có: \({x_M} = {x_o} = {{0 + 2{x_o}} \over 2} = {{{x_A} + {x_B}} \over 2}\)
Vì ba điểm A, M, B thẳng hàng nên từ đó suy ra rằng M là trung điểm của đoạn thẳng AB.
Diện tích tam giác OAB là
\(S = {1 \over 2}\left| {{y_A}} \right|\left| {{y_B}} \right| = {1 \over 2}\left| {{2 \over {{x_o}}}} \right|\left| {2{x_o} } \right|=2\,\,\,\forall {x_o} \ne 0\)
congdong.edu.vn