Lớp 12 - Toán học - Nâng cao Giải bài 10, 11, 12, 13 trang 152, 153 SGK Giải tích 12 Nâng cao
Bài 10 Trang 152 SGK Đại số và Giải tích 12 Nâng cao
Không tìm nguyên hàm hãy tính các tích phân sau:
a) \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx} ;\) \(b)\,\int\limits_{ - 1}^2 {\left| x \right|} dx\)
c) \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx\)
Hướng dẫn: Áp dụng định lí 1.
Giải
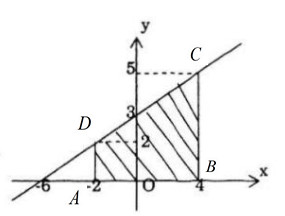
a) Tích phân đó bằng diện tích hình thang ABCD với cạnh nghiêng là đường thẳng \(y = {x \over 2} + 3.\) Diện tích đó là \(\left( {2 + 5} \right){6 \over 2} = 21.\) vậy \(\int\limits_{ - 2}^4 {\left( {{x \over 2} + 3} \right)dx = 21} .\)
b)
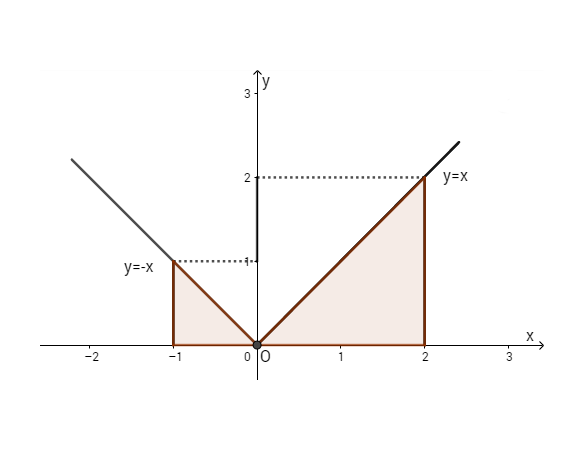
Từ hình trên ta thấy hình A gồm 2 tam giác. Do đó tích phân bằng diện tích của A và là \({1 \over 2}.1.1 + {1 \over 2}2.2 = 0,5 + 2 = 2,5\)
Vậy \(\int\limits_{ - 1}^2 {\left| x \right|} dx = {5 \over 2}\).
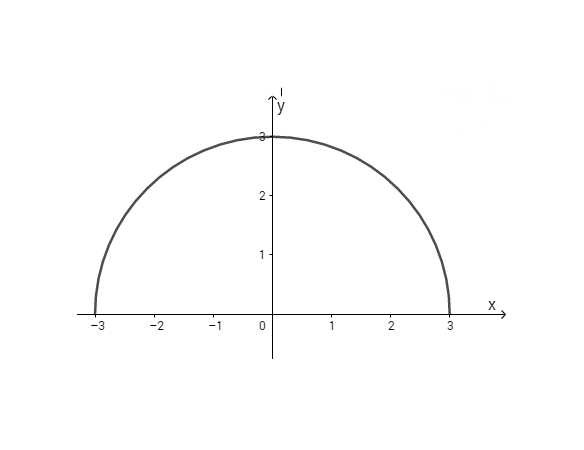
c) Tích phân bằng diện tích nửa đường tròn \({x^2} + {y^2} = 9\)(hình). Đây là đường tròn tâm là gốc tọa độ bán kính là 3. Do đó diện tích nửa dường tròn là \(9{\pi \over 2} = 4,5\pi .\)
Vậy \(\int\limits_{ - 3}^3 {\sqrt {9 - {x^2}} } dx = 4,5\pi \)
Bài 11 Trang 152 SGK Đại số và Giải tích 12 Nâng cao
Cho biết \(\int\limits_1^2 {f\left( x \right)dx = - 4,} \) \(\int\limits_1^5 {f\left( x \right)dx = 6,} \) \(\int\limits_1^5 {g\left( x \right)} dx = 8.\) hãy tính
a) \(\int\limits_2^5 {f\left( x \right)} \)
b) \(\int\limits_1^2 {3f\left( x \right)} dx\)
c) \(\int\limits_1^5 {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx\)
d) \(\int\limits_1^5 {\left[ {4f\left( x \right) - g\left( x \right)} \right]} dx \)
Giải
a) \(\int\limits_2^5 {f\left( x \right)} \)
\(= \int\limits_2^1 {f\left( x \right)} dx + \int\limits_1^5 {f\left( x \right)}dx\)
\( = - \int\limits_1^2 {f\left( x \right)} dx + \int\limits_1^5 {f\left( x \right)} dx = 4 + 6 = 10\)
b) \(\int\limits_1^2 {3f\left( x \right)} dx = 3\int\limits_1^2 {f\left( x \right)dx} = 3\left( { - 4} \right) = - 12\)
c) \(\int\limits_1^5 {\left[ {f\left( x \right) - g\left( x \right)} \right]} dx \)
\(= \int\limits_1^5 {f\left( x \right)dx} - \int\limits_1^5 {g\left( x \right)} dx = 6 - 8 = - 2\)
d) \(\int\limits_1^5 {\left[ {4f\left( x \right) - g\left( x \right)} \right]} dx \)
\(= 4\int\limits_1^5 {f\left( x \right)dx} - \int\limits_1^5 {g\left( x \right)dx = 4.6 - 8 = 16.} \)
Bài 12 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
Cho biết \(\int\limits_0^3 {f\left( z \right)dz} = 3,\int\limits_0^4 {f\left( x \right)} dx = 7.\) Hãy tính \(\int\limits_3^4 {f\left( t \right)dt.} \)
Giải
Ta có \(\int\limits_3^4 {f\left( t \right)dt = \int\limits_3^0 {f\left( t \right)} } dt + \int\limits_0^4 {f\left( t \right)} dt\)
\(= - \int\limits_0^3 {f\left( t \right)} dt + \int\limits_0^4 {f\left( t \right)} dt = - 3 + 7 = 4\)
Bài 13 Trang 153 SGK Đại số và Giải tích 12 Nâng cao
a) Chứng minh rằng nếu \(f\left( x \right) \ge 0\) trên \(\left[ {a;b} \right]\) thì \(\int\limits_a^b {f\left( x \right)dx \ge 0.} \)
b) Chứng minh rằng nếu \(f\left( x \right) \ge g\left( x \right)\) trên \(\left[ {a;b} \right]\) thì \(\int\limits_a^b {f\left( x \right)dx} \ge \int\limits_a^b {g\left( x \right)dx} .\)
Giải
a) Ta có \(\int\limits_a^b {f\left( x \right)dx} \) là diện tích hình thang cong giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b,\) do đó \(\int\limits_a^b {f\left( x \right)dx \ge 0.} \)
b) Đặt \(h\left( x \right) = f\left( x \right) - g\left( x \right) \ge 0\) với mọi \(x \in \left[ {a;b} \right].\)
Theo a) ta có: \(\int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]} \ge 0 \Rightarrow \int\limits_a^b {f\left( x \right)} dx - \int\limits_a^b {g\left( x \right)dx} \ge 0\)
\(\Rightarrow \int\limits_a^b {f\left( x \right)} dx \ge \int\limits_a^b {g\left( x \right)} dx.\)
congdong.edu.vn