Lớp 12 - Toán học - Nâng cao Bài 51, 52, 53 trang 112, 113 SGK Giải tích 12 Nâng cao

Bài 51 trang 112 SGK Đại số và Giải tích 12 Nâng cao

Giải bài tập trang 111, 112, 113 bài 5 hàm số mũ và hàm số lôgarit SGK Giải tích 12 Nâng cao.:

a) \(y = {\left( {\sqrt 2 } \right)^x}\); b) \(y = {\left( {{2 \over 3}} \right)^x}\);

Giải

a) TXĐ: \(D =\mathbb R\)

\(a = \sqrt 2 > 1\) hàm số \(y = {\left( {\sqrt 2 } \right)^x}\) đồng biến trên \(\mathbb R\)

Bảng giá trị:

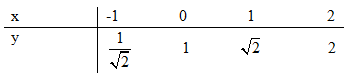
Đồ thị:

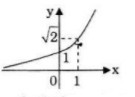
b) TXĐ: \(D =\mathbb R\)
\(a = {2 \over 3} < 0\) hàm số \(y = {\left( {{2 \over 3}} \right)^x}\) nghịch biến trên \(\mathbb R\)
Bảng giá trị:

Đồ thị:

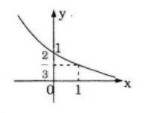
Bài 52 trang 112 SGK Đại số và Giải tích 12 Nâng cao

Sử dụng công thức \(L\left( {dB} \right) = 10\log {I \over {{I_0}}}\) (xem bài đọc thêm “Lôgarit trong một số công thức đo lường “ tr.99), hãy tính gần đúng, chính xác đến hàng đơn vị, độ lớn dB của âm thanh có tỉ số \({I \over {{I_0}}}\) cho bảng sau rồi điền vào cột còn trống:

Giải

Bài 53 trang 113 SGK Đại số và Giải tích 12 Nâng cao

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over x}\)

b) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over x}\)

Giải

a) \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over x} = 3.\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + 3x} \right)} \over {3x}} = 3\).

b) Vì \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over {{x^2}}} = 1\) nên \(\mathop {\lim }\limits_{x \to 0} {{\ln \left( {1 + {x^2}} \right)} \over x} = \mathop {\lim }\limits_{x \to 0} x{{\ln \left( {1 + {x^2}} \right)} \over {{x^2}}} = 0.1 = 0\).

                                                        congdong.edu.vn