Lớp 12 - Toán học - Nâng cao Giải bài 33, 34, 35, 36 trang 173, 174, 175 SGK Giải tích 12 Nâng cao
Bài 33 Trang 173 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt 5 {y^2},x = 0,y = - 1\) và \(y = 1\). Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
Giải
\(V = \pi \int\limits_{ - 1}^1 {(\sqrt 5 } {y^2}{)^2}dy = 5\pi \int\limits_{ - 1}^1 {{y^4}} dy = \pi {y^5}\mathop |\nolimits_{ - 1}^1 = 2\pi \)
Bài 34 Trang 174 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
Đồ thị các hàm số \(y = x, y = 1\) và \(y = {{{x^2}} \over 4}\) trong miền \(x \ge 0,y \le 1.\)
b) Đồ thị hai hàm số \(y = {x^4} - 4{x^2} + 4,y = {x^2}\), trục tung và đường thẳng \(x = 1\)
c) Đồ thị các hàm số \(y = {x^2},y = 4x - 4\) và \(y = -4x – 4\).
Giải
a)
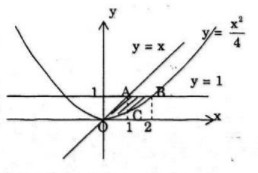
Diện tích hình thang \(OABC\) là:
\({S_1} = (2 + 1){1 \over 2} = {3 \over 2}\)
Diện tích tam giác cong \(OBC\) là hình phẳng giới hạn bởi: \(y = 0,x = 2,y = {{{x^2}} \over 4}\) là:
\({S_2} = \int\limits_0^2 {{{{x^2}} \over 4}} dx = \left. {{{{x^3}} \over {12}}} \right|_0^2 = {2 \over 3}\)
Diện tích cần tìm là \(S = {S_1} - {S_2} = {3 \over 2} - {2 \over 3} = {5 \over 6}\)
b) Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^4} - 4{x^2} + 4 = {x^2} \Leftrightarrow \left[ \matrix{
{x^2} = 1 \hfill \cr
{x^2} = 4 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
x = \pm 1 \hfill \cr
x = \pm 2 \hfill \cr} \right.\)
Ta có:
\(\eqalign{
& S = \int\limits_0^1 {\left| {{x^4} - 4{x^2} + 4 - {x^2}} \right|} dx \cr&= \int\limits_0^1 {\left| {{x^4} - 5{x^2} + 4} \right|} dx \cr
& = \int\limits_0^1 {({x^4} - 5{x^2}} + 4)dx \cr&= \left. {\left( {{{{x^5}} \over 5} - {{5{x^3}} \over 3} + 4x} \right)} \right|_0^1 = {{38} \over {15}} \cr} \)
c)

Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng \(y = 4x – 4\) là:
\(\eqalign{
& {x^2} = 4x - 4 \Leftrightarrow {x^2} - 4x + 4 = 0 \cr
& \Leftrightarrow {(x - 2)^2} = 0 \Leftrightarrow x = 2. \cr} \)
Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^2}\) và đường thẳng
\(y = -4x – 4\) là:
\(\eqalign{
& {x^2} = - 4x - 4 \Leftrightarrow {x^2} + 4x + 4 = 0 \cr
& \Leftrightarrow {(x + 2)^2} = 0 \Leftrightarrow x = - 2. \cr} \)
\(\eqalign{
& S = \int\limits_{ - 2}^0 {({x^2} + 4x + 4)} dx + \int\limits_0^2 {({x^2} - 4x + 4)} dx \cr
& = \left. {\left( {{{{x^3}} \over 3} + 2{x^2} + 4x} \right)} \right|_{ - 2}^0 + \left. {\left( {{{{x^3}} \over 3} - 2{x^2} + 4x} \right)} \right|_0^2\cr& = {8 \over 3} + {8 \over 3} = {{16} \over 3} \cr} \)
Bài 35 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hai hàm số \(y = {x^2} + 1\) và \(y = 3 – x\).
b) Các đường có phương trình \(x = {y^3}\), \(y = 1\), và \(x = 8\).
c) Đồ thị của hàm số \(y = \sqrt x ,y = 6 - x\) và trục hoành.
Giải
a) Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} + 1 = 3 - x \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 2 \hfill \cr} \right.\)
Diện tích cần tìm là:
\(\eqalign{
& S = \int\limits_{ - 2}^1 {\left| {{x^2} + 1 - (3 - x)} \right|} dx = \int\limits_{ - 2}^1 {\left| {{x^2} + x - 2} \right|} dx \cr
& = \int\limits_{ - 2}^1 {( - {x^2} - x + 2)dx = \left. {\left( { - {{{x^3}} \over 3} - {{{x^2}} \over 2} + 2x} \right)} \right|} _{ - 2}^1 \cr&= {9 \over 2} \cr} \)
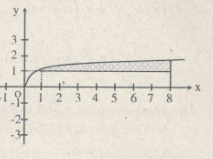
b)Diện tích cần tìm là:
\(S = \int\limits_1^8 {({x^{{1 \over 3}}} - 1)dx = \left. {\left( {{3 \over 4}{x^{{4 \over 3}}} - x} \right)} \right|_1^8} = {{17} \over 4}\)
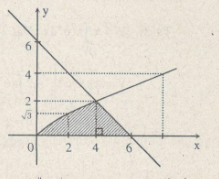
c) Phương trình hoành độ giao điểm của 2 đồ thị là:
\(\eqalign{
& \sqrt x = 6 - x \Leftrightarrow x + \sqrt x - 6 = 0 \cr
& \Leftrightarrow \sqrt x = 2 \Leftrightarrow x = 4 \cr} \)
\(S = \int\limits_0^4 {\sqrt x dx + {1 \over 2}.2.2 = \left. {{2 \over 3}{x^{{3 \over 2}}}} \right|_0^4} + 2 = {{22} \over 3}\)
Bài 36 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Tính thể tích của vật thể \(T\) nằm giữa hai mặt phẳng \(x = 0\) và \(x = \pi \), biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \((0 \le x \le \pi )\) là một hình vuông cạnh là \(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} \).
Giải
Ta có:
\(\eqalign{
& S(x) = {(2\sqrt {{\mathop{\rm s}\nolimits} {\rm{inx}}} )^2} = 4\sin x \cr
& V = \int\limits_0^\pi {S(x)dx = \int\limits_0^\pi {4\sin xdx = - 4\cos x\mathop |\nolimits_0^\pi } } = 8 \cr} \)
congdong.edu.vn