Lớp 12 - Toán học - Nâng cao Giải bài 17, 18, 19 trang 161 SGK Giải tích 12 Nâng cao
Bài 17 Trang 161 SGK Đại số và Giải tích 12 Nâng cao
Dùng phương pháp đổi biến số tính các tích phân sau:
a) \(\int\limits_0^1 {\sqrt {x + 1} dx;} \) b) \(\int\limits_0^{{\pi \over 4}} {{{\tan x} \over {{{\cos }^2}x}}} dx;\)
c) \(\int\limits_0^1 {{t^3}} {\left( {1 + {t^4}} \right)^3}dt;\) d) \(\int\limits_0^1 {{{5x} \over {{{\left( {{x^2} + 4} \right)}^2}}}} dx;\)
e) \(\int\limits_0^{\sqrt 3 } {{{4x} \over {\sqrt {{x^2} + 1} }}} dx;\) f) \(\int\limits_0^{{\pi \over 6}} {\left( {1 - \cos 3x} \right)} \sin 3xdx.\)
Giải
a) Đặt \(u = \sqrt {x + 1} \Rightarrow {u^2} = x + 1 \Rightarrow 2udu = dx.\)
Đổi cận
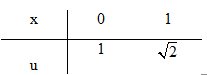
\(\int\limits_0^1 {\sqrt {x + 1} } dx = \int\limits_1^{\sqrt 2 } {u.2udu = 2\int\limits_1^{\sqrt 2 } {{u^2}du} } \)
\(= \left. {2.{{{u^3}} \over 3}} \right|_1^{\sqrt 2 } = {2 \over 3}\left( {2\sqrt 2 - 1} \right)\)
b) Đặt \(u = \tan x \Rightarrow du = {{dx} \over {{{\cos }^2}x}}\)
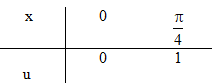
\(\int\limits_0^{{\pi \over 4}} {{{\tan x} \over {{{\cos }^2}x}}} dx = \int\limits_0^1 {udu = } \left. {{{{u^2}} \over 2}} \right|_0^1 = {1 \over 2}\)
c) Đặt \(u = 1 + {t^4} \Rightarrow du = 4{t^3}dt \Rightarrow {t^3}dt = {{du} \over 4}\)
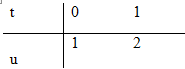
\(\int\limits_0^1 {{t^3}\left( {1 + {t^4}} \right)} dt = {1 \over 4}\int\limits_1^2 {{u^3}} du = \left. {{1 \over 4}{{{u^4}} \over 4}} \right|_1^2 = {1 \over {16}}\left( {16 - 1} \right) \)
\(= {{15} \over {16}}\)
d) Đặt \(u = {x^2} + 4 \Rightarrow du = 2xdx \Rightarrow xdx = {1 \over 2}du\)
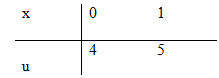
\(\int\limits_0^1 {{{5x} \over {{{\left( {{x^2} + 4} \right)}^2}}}} dx = {5 \over 2}\int\limits_4^5 {{{du} \over {{u^2}}}} = \left. {{5 \over 2}\left( { - {1 \over u}} \right)} \right|_4^5 = {1 \over 8}\)
e) Đặt \(u = \sqrt {{x^2} + 1} \Rightarrow {u^2} = {x^2} + 1 \Rightarrow udu = xdx\)
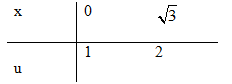
\(\int\limits_0^{\sqrt 3 } {{{4x} \over {\sqrt {{x^2} + 1} }}} dx = 4\int\limits_1^2 {{{udu} \over u}} = \left. {4u} \right|_1^2 = 4\)
f) Đặt \(u = 1 - \cos 3x \Rightarrow du = 3\sin 3xdx \)
\(\Rightarrow \sin 3xdx = {1 \over 3}du\)
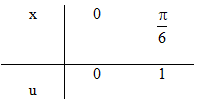
\(\int\limits_0^{{\pi \over 6}} {\left( {1 - \cos 3x} \right)} \sin 3xdx = {1 \over 3}\int\limits_0^1 {udu = \left. {{{{u^2}} \over 6}} \right|} _0^1 = {1 \over 6}\)
Bài 18 Trang 161 SGK Đại số và Giải tích 12 Nâng cao
Dùng phương pháp tích phân từng phần để tính các tích phân sau:
a) \(\int\limits_1^2 {{x^5}} \ln xdx;\) b) \(\int\limits_0^1 {\left( {x + 1} \right)} {e^x}dx;\)
c) \(\int\limits_0^\pi {{e^x}} \cos xdx;\) d) \(\int\limits_0^{{\pi \over 2}} {x\cos xdx.} \)
Giải
a) Đặt
\(\left\{ \matrix{
u = \ln x \hfill \cr
dv = {x^5}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {{dx} \over x} \hfill \cr
v = {{{x^6}} \over 6} \hfill \cr} \right.\)
\(\int\limits_1^2 {{x^5}} \ln xdx = \left. {{{{x^6}} \over 6}\ln x} \right|_1^2 - {1 \over 6}\int\limits_1^2 {{x^5}} dx \)
\(= \left. {\left( {{{{x^6}} \over 6}\ln x - {{{x^6}} \over {36}}} \right)} \right|_1^2 = {{32} \over 3}\ln 2 - {7 \over 4}\)
b) Đặt
\(\left\{ \matrix{
u = x + 1 \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
\(\int\limits_0^1 {\left( {x + 1} \right)} {e^x}dx = \left. {\left( {x + 1} \right){e^x}} \right|_0^1 - \int\limits_0^1 {{e^x}dx = e} \)
c) Đặt \(I = \int\limits_0^\pi {{e^x}\cos xdx} \)
Đặt
\(\left\{ \matrix{
u = {e^x} \hfill \cr
dv = \cos xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {e^x}dx \hfill \cr
v = {\mathop{\rm s}\nolimits} {\rm{inx}} \hfill \cr} \right.\)
Suy ra \(I = \left. {{e^x}{\mathop{\rm s}\nolimits} {\rm{inx}}} \right|_0^\pi - \int\limits_0^\pi {{e^x}\sin {\rm{x}}dx} = - \int\limits_0^\pi {{e^x}\sin {\rm{x}}dx} \)
Đặt
\(\left\{ \matrix{
u = {e^x} \hfill \cr
dv = \sin {\rm{x}}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = {e^x}dx \hfill \cr
v = - \cos x \hfill \cr} \right.\)
Do đó \(I = - \left[ {\left. {\left( { - {e^x}\cos x} \right)} \right|_0^\pi + \int\limits_0^\pi {{e^x}\cos xdx} } \right] \)
\(= {e^\pi }\cos \pi - {e^0}.\cos 0 - I\)
\( \Rightarrow 2I = - {e^\pi } - 1 \Rightarrow I = - {1 \over 2}\left( {{e^\pi } + 1} \right)\)
d) Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {\mathop{\rm s}\nolimits} {\rm{inx}} \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos xdx = \left. {x\sin x} \right|_0^{{\pi \over 2}}} - \int\limits_0^{{\pi \over 2}} {\sin {\rm{x}}dx} \)
\(= \left. {\left( {x\sin x + \cos x} \right)} \right|_0^{{\pi \over 2}} = {\pi \over 2} - 1\)
Bài 19 Trang 161 SGK Đại số và Giải tích 12 Nâng cao
Tính
a) \(\int\limits_0^1 {\sqrt {{t^5} + 2t} } \left( {2 + 5{t^4}} \right)dt;\)
b) \(\int\limits_0^{{\pi \over 2}} {x\sin {\rm{xcosx}}dx} .\)
giải
a) Đặt \(u = \sqrt {{t^5} + 2t} \Rightarrow {u^2} = {t^5} + 2t \)
\(\Rightarrow 2udu = \left( {5{t^4} + 2} \right)dt\)
\(\int\limits_0^1 {\sqrt {{t^5} + 2t} } \left( {2 + 5{t^4}} \right)dt = \int\limits_0^{\sqrt 3 } {2{u^2}du = \left. {{{2{u^3}} \over 3}} \right|} _0^{\sqrt 3 } = 2\sqrt 3 \)
b) Ta có \(I = \int\limits_0^{{\pi \over 2}} {x\sin x\cos xdx = {1 \over 2}} \int\limits_0^{{\pi \over 2}} {x\sin 2xdx} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = - {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(I = \left. {{1 \over 2}\left( { - {1 \over 2}x\cos x2x} \right)} \right|_0^{{\pi \over 2}} + {1 \over 4}\int\limits_0^{{\pi \over 2}} {\cos 2xdx}\)
\(= {\pi \over 8} + \left. {{1 \over 8}\sin 2x} \right|_0^{{\pi \over 2}} = {\pi \over 8}\)
congdong.edu.vn