Lớp 12 - Toán học - Nâng cao Giải bài 11, 12, 13 trang 53 SGK Hình học 12 Nâng cao
Bài 11 trang 53 SGK Hình học 12 Nâng cao
Chứng ming rằng hình tròn xoay có vô số mặt phẳng đối xứng.
Giải
Xét mặt tròn xoay (H) có trục là \(\Delta \). Mọi mặt phẳng \((P)\) đi qua \(\Delta \) đều là mặt phẳng đối xứng của (H). Thật vậy, nếu \(M \in \left( H \right)\) và \(M’\) là điểm đối xứng với \(M\) qua mp \((P)\) thì \(M’\) cũng nằm trên đường tròn \(\left( {{C_M}} \right)\) nên \(M' \in \left( H \right)\).
Bài 12 trang 53 SGK Hình học 12 Nâng cao
Trong mỗi trường hợp sau, gọi tên hình tròn xoay:
a) Sinh bởi ba cạnh của hình chữ nhật khi quay quanh đường thẳng chứa cạnh thứ tư.
b) Sinh bởi một hình chữ nhật (kể cả điểm trong) khi quay quanh đường thẳng chứa một cạnh.
Giải
a) Hình trụ.
b) Khối trụ.
Bài 13 trang 53 SGK Hình học 12 Nâng cao
Cho đường tròn \((O;R)\) nằm trong mặt phẳng \((P)\). Tìm tập hợp các điểm \(M\) trong không gian sao cho hình chiếu của chúng trên \((P)\) luôn nằm trên đường tròn đã cho.
Giải
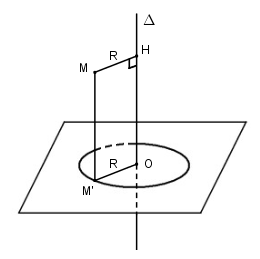
Gọi \(\Delta \) là trục của đường tròn \((O;R)\). Hình chiếu \(M’\) của \(M\) nằm trên \((O;R)\) thì \(MM’ // \Delta \) và khoảng cách từ \(M\) tới \(\Delta \) bằng \(MO’ = R\).
Vậy tập hợp các điểm \(M\) là hình trụ có trục là \(\Delta \) và có bán kính bằng \(R\).
congdong.edu.vn