Lớp 12 - Toán học - Nâng cao Giải bài 31, 32, 33 trang 206, 207 SGK Giải tích 12 Nâng cao

Bài 31 trang 206 SGK giải tích 12 nâng cao

Cho các số phức \({\rm{w}}= {{\sqrt 2 } \over 2}\left( {1 + i} \right)\) và \(\varepsilon = {1 \over 2}\left( { - 1 + i\sqrt 3 } \right)\)

a) Chứng minh rằng \({z_o} = \cos {\pi \over {12}} + i\sin {\pi \over {12}},\,{z_1} = {z_o}\varepsilon ,\,{z_2} = {z_o}{\varepsilon ^2}\) là các nghiệm của phương trình \({z^3} - {\rm{w}} = 0;\)

b) Biểu diễn hình học các số phức \({z_o},\,{z_1},\,{z_2}\)

Giải

a) Ta có: \({\rm{w}} = \cos {\pi \over 4} + i\sin {\pi \over 4}\)

\(\eqalign{ & \varepsilon = \cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3} \cr & z_o^3 = {\left( {\cos {\pi \over {12}} + i\sin {\pi \over {12}}} \right)^3} = \cos {\pi \over 4} + i\sin {\pi \over 4} ={\rm{w}} \cr & z_1^3 = {\left( {{z_o}\varepsilon } \right)^3} = z_o^3.{\varepsilon ^3} = {\rm{w}} \,\,\left( {\text{vì}\,\,\,{\varepsilon ^3} = 1} \right), \cr & z_2^3 = {\left( {z_o{\varepsilon ^2}} \right)^3} = z_o^3{\varepsilon ^6} = z_o^3 ={\rm{w}}\cr} \)

b) Biểu diễn: Các điểm A, B, C lần lượt biểu diễn \({z_0},\,\,{z_1},\,\,{z_2}\)

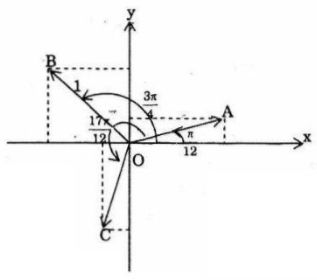
Nhận xét: A,B,C tạo thành một tam giác đều.

Bài 32 trang 207 SGK giải tích 12 nâng cao

Sử dụng công thức Moa-vrơ để tính \(\sin 4\varphi \) và \(\cos 4\varphi \) theo các lũy thừa của \(\sin \varphi \) và \(\cos \varphi \)

Giải

Ta có: \(\cos 4\varphi + i\sin 4\varphi = {\left( {\cos \varphi + i\sin \varphi } \right)^4}\)

\(\eqalign{ & = {\cos ^4}\varphi + 4\left( {{{\cos }^3}\varphi } \right)\left( {i\sin \varphi } \right) \cr&+ 6\left( {{{\cos }^2}\varphi } \right)\left( {{i^2}} \right){\sin ^2}\varphi \cr&+ 4\left( {\cos \varphi } \right)\left( {{i^3}{{\sin }^3}\varphi } \right) + {i^4}{\sin ^4}\varphi \cr & = {\cos ^4}\varphi - 6{\cos ^2}\varphi {\sin ^2}\varphi + {\sin ^4}\varphi \cr&+ \left( {4{{\cos }^3}\varphi \sin \varphi - 4\cos \varphi {{\sin }^3}\varphi } \right)i. \cr} \)

Từ đó: \(\cos 4\varphi = {\cos ^4}\varphi - 6{\cos ^2}\varphi {\sin ^2}\varphi + {\sin ^4}\varphi \)

\(\sin 4\varphi = 4{\cos ^3}\varphi \sin \varphi - 4\cos \varphi {\sin ^3}\varphi \)

Bài 33 trang 207 SGK giải tích 12 nâng cao

Tính \({\left( {\sqrt 3 - i} \right)^6};\,\,\,{\left( {{i \over {1 + i}}} \right)^{2004}};\,\,\,{\left( {{{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }}} \right)^{21}}\)

Giải

\({\left( {\sqrt 3 - i} \right)^6} = {\left[ {2\left( {\cos \left( { - {\pi \over 6}} \right) + i\sin \left( { - {\pi \over 6}} \right)} \right)} \right]^6}\)

\(= {2^6}\left[ {\cos \left( { - \pi } \right) + i\sin \left( { - \pi } \right)} \right] = - {2^6}\)

\({i \over {i + 1}} = {{1 + i} \over 2} = {1 \over {\sqrt 2 }}\left( {\cos {\pi \over 4} + i\sin {\pi \over 4}} \right)\) nên

\(\eqalign{ & {\left( {{1 \over {1 + i}}} \right)^{2004}} = {1 \over {{2^{1002}}}}\left( {\cos {{2004\pi } \over 4} + i\sin {{2004\pi } \over 4}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {1 \over {{2^{1002}}}}\left( {\cos \pi + i\sin \pi } \right) = - {1 \over {{2^{1002}}}} \cr} \)

\({{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }} = {{\left( {5 + 3i\sqrt 3 } \right)\left( {1 + 2i\sqrt 3 } \right)} \over {1 + 12}} = {{ - 13 + 13i\sqrt 3 } \over {13}} \)

\(= - 1 + i\sqrt 3 \)

\( = 2\left( { - {1 \over 2} + {{\sqrt 3 } \over 2}i} \right) = 2\left( {\cos {{2\pi } \over 3} + i\sin {{2\pi } \over 3}} \right)\)

Do đó:

\({\left( {{{5 + 3i\sqrt 3 } \over {1 - 2i\sqrt 3 }}} \right)^{21}} = {2^{21}}\left( {\cos 14\pi + i\sin 14\pi } \right) = {2^{21}}\)

                                                                                                  congdong.edu.vn