Lớp 12 - Toán học - Nâng cao Giải bài 45, 46, 47, 48 trang 176 SGK Giải tích 12 Nâng cao
Bài 45 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Xác định số b dương để tích phân \(\int\limits_0^b {\left( {x - {x^2}} \right)dx} \) có giá trị lớn nhất.
Giải
Ta có \(\int\limits_0^b {\left( {x - {x^2}} \right)} dx = \left. {\left( {{{{x^2}} \over 2} - {{{x^3}} \over 3}} \right)} \right|_0^b = {{{b^2}} \over 2} - {{{b^3}} \over 3}\)
Xét hàm số \(I\left( b \right) = {{{b^2}} \over 2} - {{{b^3}} \over 3}\) với \(b>0\)
ta có
\(\eqalign{
& I'\left( b \right) = b - {b^2} \cr
& I'\left( b \right) = 0 \Leftrightarrow b = 0;b = 1 \cr} \)
Bảng biến thiên
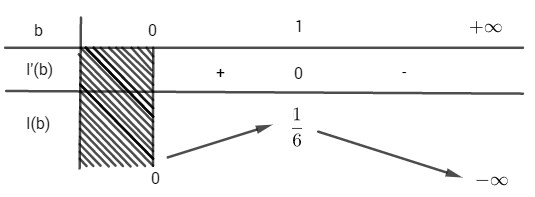
\( I(b)\) đạt giá trị lớn nhất bằng \({1\over 6}\) khi \(b=1\)
Bài 46 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Cho biết \(\int\limits_1^9 {f\left( x \right)dx} = - 1,\int\limits_7^9 {f\left( x \right)} dx = 5,\int\limits_7^9 {g\left( x \right)} dx = 4.\)
Hãy tìm:
a) \(\int\limits_1^9 { - 2f\left( x \right)} dx;\) \(b)\,\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx;\)
\(c)\,\int\limits_7^9 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx;} \) \(d)\,\int\limits_1^7 {f\left( x \right)} dx;\)
Giải
a) \(\int\limits_1^9 { - 2f\left( x \right)} dx = - 2\int\limits_1^9 {f\left( x \right)dx = - 2\left( { - 1} \right)} = 2\)
b) \(\int\limits_7^9 {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx = \int\limits_7^9 {f\left( x \right)} dx + \int\limits_7^9 {g\left( x \right)} dx\)
\(= 5 + 4 = 9\)
c) \(\int\limits_7^9 {\left[ {2f\left( x \right) - 3g\left( x \right)} \right]dx = } 2\int\limits_7^9 {f\left( x \right)} dx - 3\int\limits_7^9 {g\left( x \right)} dx \)
\(= 2.5 - 3.4 = - 2\)
d) \(\int\limits_1^7 {f\left( x \right)} dx = \int\limits_1^9 {f\left( x \right)} dx + \int\limits_9^7 {f\left( x \right)} dx\)
\(= \int\limits_1^9 {f\left( x \right)} dx - \int\limits_7^9 {f\left( x \right)} dx = - 1 - 5 = - 6\)
Bài 47 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Cho hàm số f liên tục trên \(\left[ {a;b} \right].\) Tỉ số : \({1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx\) được gọi là giá trị trung bình của hàm số f trên \(\left[ {a;b} \right]\) và được kí hiệu là \(m\left( f \right)\). Chứng minh rằng tồn tại điểm \(c \in \left[ {a;b} \right]\) sao cho \(m\left( f \right) = f\left( c \right)\)
Giải
Giả sử m và M tương ứng là giá trị bé nhất và lớn nhất của hàm số f trên \(\left[ {a;b} \right]\).
Ta có \(m \le f\left( x \right) \le M\,\,\forall x \in \left[ {a;b} \right]\)
Theo kết quả
\(f(x)>g(x)\) trên đoạn \([a;b]\) thì \(\int\limits_a^b {f(x)} dx > \int\limits_a^b {g(x)dx} \)
Ta có:
\(\eqalign{
& \int\limits_a^b {mdx \le \int\limits_a^b {f\left( x \right)dx} } \le \int\limits_a^b {Mdx}\cr& \Rightarrow m\left( {b - a} \right) \le \int\limits_a^b {f\left( x \right)dx \le M\left( {b - a} \right)} \cr
& \Rightarrow m \le {1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx \le M \cr} \)
Vì \(f\) là hàm liên tục nên tồn tại \(c \in \left[ {a;b} \right]\) để \(f\left( c \right) = {1 \over {b - a}}\int\limits_a^b {f\left( x \right)} dx.\)
Bài 48 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Giả sử một vật từ trạng thái nghỉ khi \(t=0\) (s) chuyển động thẳng với vận tốc \(v\left( t \right) = t\left( {5 - t} \right)\,\,\,\left( {m/s} \right)\). Tìm quãng đường vật đi được cho tới khi nó dừng lại.
Giải
Ta có
\(v\left( t \right) = 0 \Leftrightarrow \left[ \matrix{
t = 0 \hfill \cr
t = 5 \hfill \cr} \right.\)
Vật dừng lại tại thời điểm \(t=5\). Quãng đường vật đi được là
\(S = \int\limits_0^5 {t\left( {5 - t} \right)} dt = \left. {\left( {{{5{t^2}} \over 2} - {{{t^3}} \over 3}} \right)} \right|_0^5 = {{125} \over 6}\,\,\,\left( m \right)\)
congdong.edu.vn