Lớp 12 - Toán học - Nâng cao Giải bài 60, 61, 62 trang 117, 118 SGK Giải tích 12 Nâng cao
Bài 60 SGK giải tích 12 nâng cao trang 117
a) Chứng minh rằng đồ thị của hai hàm số \(y = {a^x};\,y = {\left( {{1 \over a}} \right)^x}\) đối xứng với nhau qua trục tung.
b) Chứng minh rằng đồ thị của hai hàm số \(y = {\log _a}x;\,\,y = {\log _{{1 \over a}}}x\) đối xứng với nhau qua trục hoành.
Giải
a) Gọi \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) lần lượt là đồ thị củ hàm số \(y = {a^x};\,y = {\left( {{1 \over a}} \right)^x}\), \(M\left( {{x_o},{y_o}} \right)\) là một điểm bất kì. Khi đó điểm đối xứng với M qua trục tung là \(M'\left( { - {x_o},{y_o}} \right)\).
Ta có: \(M \in \left( {{G_1}} \right) \Leftrightarrow {y_o} = {a^{{x_o}}} \Leftrightarrow {y_o}={\left( {{1 \over a}} \right)^{ - {x_o}}} \)
\(\Leftrightarrow M' \in \left( {{G_2}} \right)\)
Điều đó chứng tỏ \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) đối xứng với nhau qua trục tung.
b) Gọi \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) lần lượt là đồ thị củ hàm số \(y = {\log _a}x;\,\,y = {\log _{{1 \over a}}}x\)
Lấy \(M\left( {{x_o},{y_o}} \right)\) tùy ý. Điểm đối xứng với M qua trục hoành là \(M'\left( {{x_o}, - {y_o}} \right)\).
Ta có: \(M \in \left( {{G_1}} \right) \Leftrightarrow {y_o} = {\log _a}{x_o} = - {\log _{{1 \over a}}}{x_o} \)
\(\Leftrightarrow - {y_o} = {\log _{{1 \over a}}}{x_o} \Leftrightarrow M' \in \left( {{G_2}} \right)\)
Vậy \(\left( {{G_1}} \right)\) và \(\left( {{G_2}} \right)\) đối xứng với nhau qua trục hoành.
Bài 61 SGK giải tích 12 nâng cao trang 118
a) Vẽ đồ thị hàm số \(y = {\log _{0,5}}x > 0;\)
b) \( - 3 \le {\log _{0,5}}x \le - 1\)
Giải
a) TXĐ: \(D = \left( {0; + \infty } \right)\)
a = 0,5 < 1. Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
Bảng giá trị:
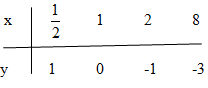
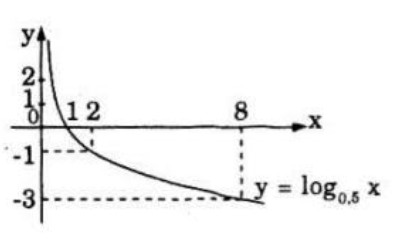
b) \({\log _{0,5}}x > 0 \Leftrightarrow 0 < x < 1\) (ứng với phần đồ thị ở phía trên trục hoành).
c) \( - 3 < {\log _{0,5}}x < - 1 \Leftrightarrow 2 < x \le 8\) (ứng với những điểm trên đồ thị có tung độ thuộc nửa khoảng \(\left[ { - 3;1} \right)\)).
Bài 62 SGK giải tích 12 nâng cao trang 118
Vẽ đồ thị của hàm số \(y = {\left( {\sqrt 3 } \right)^x}\). Dựa vào đồ thị, hãy giải thích các bất phương trình sau:
a) \({\left( {\sqrt 3 } \right)^x} \le 1\); b) \({\left( {\sqrt 3 } \right)^x} > 3\)
Giải
TXĐ: \(D =\mathbb R\)
Hàm số đồng biến trên R.
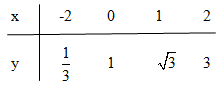
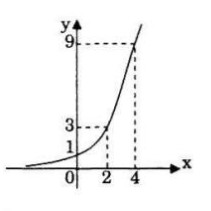
a) \({\left( {\sqrt 3 } \right)^x} \le 1 \Leftrightarrow x \le 0\) (ứng với những điểm trên đồ thị có tung độ lớn hơn 1)
b) \({\left( {\sqrt 3 } \right)^x} > 3 \Leftrightarrow x > 2\) (ứng với những điểm trên đồ thị có tung độ lón hơn 3).
congdong.edu.vn