Lớp 12 - Toán học - Nâng cao Giải bài 37, 38, 39, 40 trang 175 SGK Giải tích 12 Nâng cao
Bài 37 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng \(A\) giới hạn bởi các đường \(y = {x^2},x = 0\) và \(x = 2\). Tính thể tích của khối tròn xoay tạo thành khi quay hình \(A\) quanh trục hoành.
Giải
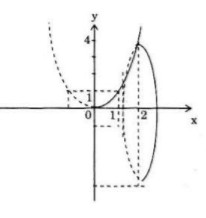
Ta có:
\(V = \pi \int\limits_0^2 {{x^4}dx = \left. {\pi .{{{x^5}} \over 5}} \right|_0^2 = {{32\pi } \over 5}} \)
Bài 38 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng A giới hạn bởi các đường \(y = \cos x, y = 0, x = 0\) và \(x = {\pi \over 4}.\)
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Giải
Ta có:
\(\eqalign{
& V = \pi \int\limits_0^{{\pi \over 4}} {{{\cos }^2}xdx = {\pi \over 2}\int\limits_0^{{\pi \over 4}} {(1 + \cos 2x)dx} } \cr
& = {\pi \over 2}\left. {\left( {x + {1 \over 2}\sin 2x} \right)} \right|_0^{{\pi \over 4}} = {\pi \over 2}\left( {{\pi \over 4} + {1 \over 2}} \right) \cr&= {{\pi (\pi + 2)} \over 8} \cr} \)
Bài 39 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng A giới hạn bởi các đường \(y = x{e^{{x \over 2}}},y = 0,x = 0\) và \(x = 1\).
Tính thể tích của khối tròn xoay tạo thành khi quay hình A quanh trục hoành.
Giải
Ta có: \(V = \pi \int\limits_0^1 {{x^2}{e^x}dx} \). Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
\(V = \pi \left( {{x^2}{e^x}\mathop |\nolimits_0^1 - 2\int\limits_0^1 {x{e^x}dx} } \right) = \pi \left( {e - 2{I_1}} \right)\)
Với \({I_1} = \int\limits_0^1 {x{e^x}dx} \). Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = {e^x}dx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {e^x} \hfill \cr} \right.\)
Do đó \({I_1} = x{e^x}\mathop |\nolimits_0^1 - \int\limits_0^1 {{e^x}dx = e - {e^x}\mathop |\nolimits_0^1 } = 1\).
Vậy \(V = \pi \left( {e - 2} \right).\)
Bài 40 Trang 175 SGK Đại số và Giải tích 12 Nâng cao
Cho hình phẳng B giới hạn bởi các đường \(x = \sqrt {2\sin 2y} ,x = 0,y = 0\) và \(y = {\pi \over 2}.\)
Tính thể tích của khối tròn xoay tạo thành khi quay hình B quanh trục tung.
Giải
Ta có: \(V = \pi \int\limits_0^{{\pi \over 2}} {2\sin 2ydy = - \pi \cos 2y\mathop |\nolimits_0^{{\pi \over 2}} } = 2\pi \)
congdong.edu.vn