Lớp 12 - Toán học - Nâng cao Giải bài 49, 50, 51, 52 trang 176, 177 SGK Giải tích 12 Nâng cao
Bài 49 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Một chất điểm A xuất phát từ vị trí O, chuyển động thẳng nhanh dần đều; 8 giây sau nó đạt đến vận tốc 6 m/s. từ thời điểm đó nó chuyển động thẳng đều. Một chất điểm B xuất phát từ cùng vị trí O nhưng chậm hơn 12 giây so với A và chuyển động thẳng nhanh dần đều. biết rằng B đuổi kịp A sau 8 giây ( kể từ lúc B xuất phát). Tìm vận tốc của B tại thời điểm đuổi kịp A.
Giải
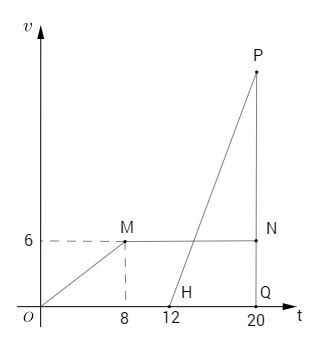
Thời điểm A và B gặp nhau là 20 giây kể từ lúc A xuất phát. Đồ thị của vận tốc của A là đường gấp khúc OMN.
Quãng đường mà A đi được (s = vt ) là diện tích hình thang OMNQ.
\({S_{OMNQ}} = {1 \over 2}\left( {20 + 12} \right).6 = 96\)
Vậy lúc gặp B, A đi được \(96 m\).
Đồ thị vận tốc của B là đường thẳng HP. Vì B xuất phát cùng vị trí với A nên B cũng đi được \(96 m\) . Quãng đường B đi được bằng diện tích tam giác \(HPQ\).
Ta có \({S_{HPQ}} = {1 \over 2}.PQ.HQ \Rightarrow 96 = {1 \over 2}.PQ.8 \Rightarrow PQ = 24.\)
Vậy vận tốc của B tại thời điểm gặp A là \(24\, m/s\).
Bài 50 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Tính các tích phân sau:
\(a)\,\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx;} \) \(b)\,\int\limits_1^2 {x\left( {2{x^2} + 1} \right)} dx;\)
\(c)\,\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx.\)
Giải
a) Đặt
\(\left\{ \matrix{
u = {x^2} \hfill \cr
dv = \sin 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = 2xdx \hfill \cr
v = - {1 \over 2}\cos 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx} = \left. { - {1 \over 2}{x^2}\cos 2x} \right|_0^{{\pi \over 2}} + \int\limits_0^{{\pi \over 2}} {{x^2}\cos 2xdx} \)
\( = {{{\pi ^2}} \over 8} + \int\limits_0^{{\pi \over 2}} {x\cos 2xdx\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)} \)
Đặt
\(\left\{ \matrix{
u = x \hfill \cr
dv = \cos 2xdx \hfill \cr} \right. \Rightarrow \left\{ \matrix{
du = dx \hfill \cr
v = {1 \over 2}\sin 2x \hfill \cr} \right.\)
Do đó \(\int\limits_0^{{\pi \over 2}} {x\cos 2xdx\, = \left. {{1 \over 2}x\sin 2x} \right|_0^{{\pi \over 2}}} - {1 \over 2}\int\limits_0^{{\pi \over 2}} {\sin 2xdx} \)
\(= \left. {{1 \over 4}\cos 2x} \right|_0^{{\pi \over 2}} = - {1 \over 2}\,\,\,\,\,\,\,\,\left( 2 \right)\)
Thay (2) vào (1) ta được: \(\int\limits_0^{{\pi \over 2}} {{x^2}\sin 2xdx = {{{\pi ^2}} \over 8}} - {1 \over 2}.\)
b) Đặt \(u = 2{x^2} + 1 \Rightarrow du = 4xdx \Rightarrow xdx = {{du} \over 4}\)
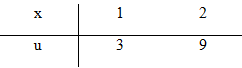
\(\int\limits_1^2 {x\left( {2{x^2} + 1} \right)dx = {1 \over 4}} \int\limits_3^9 {udu} = \left. {{1 \over 8}{u^2}} \right|_3^9 = 9\)
c) Đặt \(u = {x^2} - 2x \Rightarrow du = 2\left( {x - 1} \right)dx\)
\(\Rightarrow \left( {x - 1} \right)dx = {{du} \over 2}\)
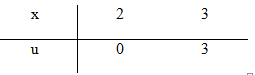
\(\int\limits_2^3 {\left( {x - 1} \right)} {e^{{x^2} - 2x}}dx = {1 \over 2}\int\limits_0^3 {{e^u}du = } \left. {{1 \over 2}{e^u}} \right|_0^3 = {1 \over 2}\left( {{e^3} - 1} \right)\)
Bài 51 Trang 176 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích các hình phẳng giới hạn bởi:
a) Đồ thị các hàm số \(y = 4 - {x^2},y = - x + 2;\)
b) Các đường cong có phương trình \(x = 4 - 4{y^2}\) và \(x = 1 - {y^4}\) trong miền \(x\ge0\).
Giải
a) Phương trình hoành độ giao điểm của hai đồ thị là:
\(4 - {x^2} = - x + 2 \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ \matrix{
x = - 1 \hfill \cr
x = 2 \hfill \cr} \right.\)
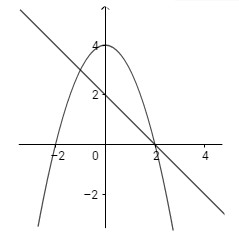
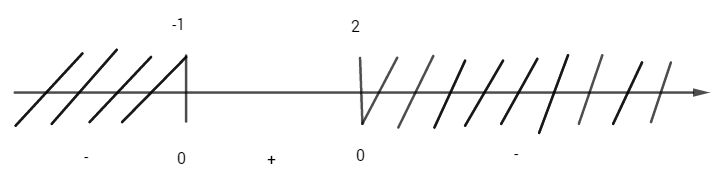
Do đó
\(\eqalign{
& S = \int\limits_{ - 1}^2 {\left| {4 - {x^2} - \left( { - x + 2} \right)} \right|} dx \cr&= \int\limits_{ - 1}^2 {\left| { - {x^2} + x + 2} \right|} dx \cr
& = \int\limits_{ - 1}^2 {\left( { - {x^2} + x + 2} \right)} dx = \left. {\left( { - {{{x^3}} \over 3} + {{{x^2}} \over 2} + 2x} \right)} \right|_{ - 1}^2 \cr& = {9 \over 2} \cr} \)
b) Phương trình tung độ giao điểm của hai đồ thị là
\(4 - 4{y^2} = 1 - {y^4} \Leftrightarrow {y^4} - 4{y^2} + 3 = 0 \)
\(\Leftrightarrow \left[ \matrix{
{y^2} = 1 \hfill \cr
{y^2} = 3 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
y = \pm 1 \hfill \cr
y = \pm \sqrt 3\; (\text{ loại vì } x<0)\hfill \cr} \right.\)
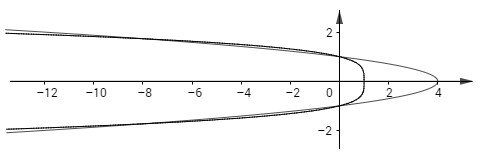
Diện tích giới hạn hai đồ thị ở phần \(x \ge 0\) là:
\(\eqalign{
& S = \int\limits_{ - 1}^1 {\left[ {4 - 4{y^2} - \left( {1 - {y^4}} \right)} \right]} dy \cr
& \,\,\, = \int\limits_{ - 1}^1 {\left( {{y^4} - 4{y^2} + 3} \right)} dy \cr
& \,\, = \left. {\left( {{{{y^5}} \over 5} - {4 \over 3}{y^3} + 3y} \right)} \right|_{ - 1}^1 = 2.{{28} \over {15}} = {{56} \over {15}} \cr} \)
Bài 52 Trang 177 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích của các hình phẳng giới hạn bởi:
a) Parabol \(y = {x^2} - 2x + 2,\) tiếp tuyến của nó tại điểm \(M(3;5)\) và trục tung;
b) Parabol \(y = - {x^2} + 4x - 3\) và các tiếp tuyến của nó tại các điểm \(A(0;-3)\) và \(B(3;0)\)
Giải
a)
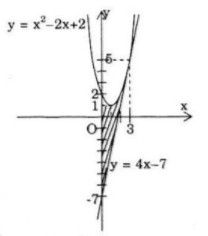
Ta có \(y' = 2x - 2 \Rightarrow y'\left( 3 \right) = 4.\)
Phương trình tiếp tuyến với parabol tại M(3;5) là:
\(y - 5 = 4\left( {x - 3} \right) \Leftrightarrow y = 4x - 7\)
Gọi S là diện tích cần tìm, ta có :
\(\eqalign{
& S = \int\limits_0^3 {\left( {{x^2} - 2x + 2 - 4x + 7} \right)} dx \cr
& \,\,\, = \int\limits_0^3 {\left( {{x^2} - 6x + 9} \right)} dx = \int\limits_0^3 {{{\left( {x - 3} \right)}^2}dx} \cr
& \,\,\, = \left. {{1 \over 3}{{\left( {x - 3} \right)}^3}} \right|_0^3 = 9. \cr} \)
b)
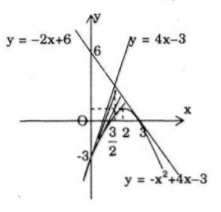
Ta có \(y' = - 2x + 4 \Rightarrow y'\left( 0 \right) = 4;y'\left( 3 \right) = - 2\)
Phương trình tiếp tuyến tại \(A(0;3)\) là :
\(y + 3 = 4\left( {x - 0} \right) \Leftrightarrow y = 4x - 3\)
Phương trình tiếp tuyến tại \(B(3;0)\) là :
\(y = - 2\left( {x - 3} \right) \Leftrightarrow y = - 2x + 6\)
Giao điểm của hai tiếp tuyến là \(C\left( {{3 \over 2};3} \right).\) kí hiệu \({A_1}\) và \({A_2}\) là tam giác cong \(ACD\) Và \(BCD\). Ta có :
\(S\left( {{A_1}} \right) = \int\limits_0^{{3 \over 2}} {\left( {4x - 3 + {x^2} - 4x + 3} \right)} dx \)
\(= \int\limits_0^{{3 \over 2}} {{x^2}dx = \left. {{{{x^3}} \over 3}} \right|_0^{{3 \over 2}}} = {9 \over 8}\)
\(S\left( {{A_2}} \right) = \int\limits_{{3 \over 2}}^3 {\left( { - 2x + 6 + {x^2} - 4x + 3} \right)} dx \)
\(= \int\limits_{{3 \over 2}}^3 {{{\left( {x - 3} \right)}^2}dx = } \left. {{1 \over 3}{{\left( {x - 3} \right)}^3}} \right|_{{3 \over 2}}^3 = {9 \over 8}\)
Vậy \(S = S\left( {{A_1}} \right) + S\left( {{A_2}} \right) = {9 \over 8} + {9 \over 8} = {9 \over 4}\)
congdong.edu.vn