Lớp 12 - Toán học - Nâng cao Giải bài 26, 27, 28 trang 167 SGK Giải tích 12 Nâng cao
Bài 26 trang 167 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = {\mathop{\rm s}\nolimits} {\rm{inx}} + 1\), trục hoành và hai đường thẳng \(x=0\) và \(x = {{7\pi } \over 6}\)
Giải
Vì \({\mathop{\rm s}\nolimits} {\rm{inx}} + 1 \ge 0\) với mọi \(x\) nên
\(S = \int\limits_0^{{{7\pi } \over 6}} {\left( {{\mathop{\rm s}\nolimits} {\rm{inx}} + 1} \right)} dx = \left. {\left( { - \cos x + x} \right)} \right|_0^{{{7\pi } \over 6}}\)
\(= {{7\pi } \over 6} + {{\sqrt 3 } \over 2} + 1\)
Bài 27 Trang 167 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị hàm số \(y = {\cos ^2}x,\) trục hoành, trục tung và đường thẳng \(x = \pi ;\)
b) Đồ thị hai hàm số \(y = \sqrt x \) và \(y = \root 3 \of x ;\)
c) Đồ thị hàm số \(y = 2{x^2}\) và \(y = {x^4} - 2{x^2}\) trong miền \(x \ge 0.\)
Giải
a) \(S = \int\limits_0^\pi {{{\cos }^2}xdx = {1 \over 2}} \int\limits_0^\pi {\left( {1 + \cos 2x} \right)} dx\)
\(= \left. {{1 \over 2}\left( {x + {1 \over 2}\sin 2x} \right)} \right|_0^\pi = {\pi \over 2}\)
b) Phương trình hoành độ giao điểm của hai đồ thị là \(\sqrt x = \root 3 \of x \Leftrightarrow x = 0;x = 1\)
Trên đoạn \(\left[ {0;1} \right]\) thì \(\root 3 \of x \ge \sqrt x \) nên:
\(S = \int\limits_0^1 {\left( {\root 3 \of x - \sqrt x } \right)} dx = \int\limits_0^1 {\left( {{x^{{1 \over 3}}} - {x^{{1 \over 2}}}} \right)} dx\)
\(= \left. {\left( {{3 \over 4}{x^{{4 \over 3}}} - {2 \over 3}{x^{{3 \over 2}}}} \right)} \right|_0^1 = {3 \over 4} - {2 \over 3} = {1 \over {12}}\)
c) Trong miền \(x \ge 0\) hoành độ giao điểm của hai đồ thị là nghiệm phương trình:
\(\left\{ \matrix{
x \ge 0 \hfill \cr
{x^4} - 2{x^2} = 2{x^2} \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge 0 \hfill \cr
{x^2}\left( {{x^2} - 4} \right) = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 2 \hfill \cr} \right.\)
Ta có: \(S = \int\limits_0^2 {\left| {{x^4} - 2{x^2} - 2{x^2}} \right|} dx = \int\limits_0^2 {\left| {{x^2}\left( {{x^2} - 4} \right)} \right|} dx \)
\(= \int\limits_0^2 {\left( {4{x^2} - {x^4}} \right)} dx\)
\( = \left. {\left( {4{{{x^3}} \over 3} - {{{x^5}} \over 5}} \right)} \right|_0^2 = {{64} \over {15}}\)
Bài 28 Trang 167 SGK Đại số và Giải tích 12 Nâng cao
Tính diện tích hình phẳng giới hạn bởi:
a) Đồ thị các hàm số \(y = {x^2} - 4\), \(y = - {x^2} - 2x\) và đường thẳng \(x = - 3,x = - 2;\)
b) Đồ thị hai hàm số \(y = {x^2}\) và \(y = - {x^2} - 2x\)
c) Đồ thị hàm số \(y = {x^3} - 4x\), trục hoành, đường thẳng x=-2 và đường thẳng x=4
Giải
a) Ta có
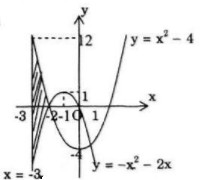
\(S = \int\limits_{ - 3}^{ - 2} {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx \)
\(= \int\limits_{ - 3}^{ - 2} {\left( {2{x^2} + 2x - 4} \right)} dx\)
\( = 2\int\limits_{ - 3}^{ - 2} {\left( {{x^2} + x - 2} \right)} dx\) vì \(({x^2} + x - 2 \ge 0 \Leftrightarrow x \le - 2\) hoặc \(x \ge 1)\)
\( = 2\left. {\left( {{{{x^3}} \over 3} + {{{x^2}} \over 2} - 2x} \right)} \right|_{ - 3}^{ - 2} = {{11} \over 3}\)
b)Phương trình hoành độ giao điểm của hai đồ thị là:
\({x^2} - 4 = - {x^2} - 2x \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 1 \hfill \cr} \right.\)
Do đó \(S = \int\limits_{ - 2}^1 {\left| {{x^2} - 4 - \left( { - {x^2} - 2x} \right)} \right|} dx \)
\(= \int\limits_{ - 2}^1 {\left| {2{x^2} + 2x - 4} \right|} dx\)
\( = - \int\limits_{ - 2}^1 {\left( {2{x^2} + 2x - 4} \right)} dx\) ( vì \( - 2 \le x \le 1 \Leftrightarrow 2{x^2} + 2x - 4 \le 0\))
\( = \int\limits_{ - 2}^1 {\left( { - 2{x^2} - 2x + 4} \right)} dx \)
\(= \left. {\left( { - {{2{x^3}} \over 3} - {x^2} + 4x} \right)} \right|_{ - 2}^1 = 9\)
c) \(S = \int\limits_{ - 2}^4 {\left| {{x^3} - 4x} \right|} dx \)
\(= \int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)} dx - \int\limits_0^2 {\left( {{x^3} - 4x} \right)} dx \)
\(+ \int\limits_2^4 {\left( {{x^3} - 4x} \right)} dx = 44\)
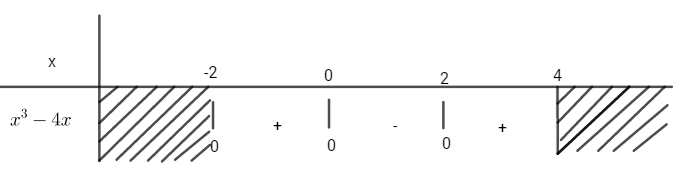
congdong.edu.vn