Bài 1 trang 68 - SGK Hình học 12
Cho ba vectơ \(\overrightarrow{a}\)(2; -5; 3), \(\overrightarrow{b}\)(0; 2; -1), \(\overrightarrow{c}\)(1; 7; 2).
a) Tính tọa độ của vectơ \(\overrightarrow{d}=4.\overrightarrow{a}-\frac{1}{3}\overrightarrow{b}+3\overrightarrow{c}\).
b) Tính tọa độ của vectơ \(\overrightarrow{e}=\overrightarrow{a}-4\overrightarrow{b}-2\overrightarrow{c}\).
Giải:
a) \(4\overrightarrow{a}=( 8; -20; 12)\); \(\frac{1}{3}\overrightarrow{b}= (0;\frac{2}{3}; \frac{-1}{3})\) ; \(2\overrightarrow{c} = ( 3; 21; 6)\).
Vậy \(\overrightarrow{d}=(11; \frac{1}{3};\frac{55}{3})\).
b) Tương tự \(\overrightarrow{e}=( 0; -27; 3)\).
Bài 2 trang 68 - SGK Hình học 12
Cho ba điểm \(A = (1; -1; 1), B = (0; 1; 2), C = (1; 0; 1)\).
Tìm tọa độ trọng tâm \(G\) của tam giác \(ABC\).
Giải:
\(G\) là trọng tâm của tam giác ABC thì \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\) (*)
Giả sử \(G(x; y; z)\) thì \(\overrightarrow{GA} = (1 - x; -1 - y; 1 - z)\);
\(\overrightarrow{GB} = (-x; 1 - y; 2 - z)\);
\(\overrightarrow{GC} = (1 - x; -y; 1 - z)\);
=> \(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC} = (2 - 3x; -3y; 4 - 3z)\)
Do hệ thức (*), ta có :
\(2 - 3x = 0 \Rightarrow x = \frac{2}{3}\) ;
\(-3y = 0 \Rightarrow y = 0\);
\( 4 - 3z = 0 \Rightarrow z = \frac{4}{3}\).
Vậy \(G(\frac{2}{3};0;\frac{4}{3})\).
Nhận xét : Trọng tâm \(G\) của tam giác \(ABC\) bằng trung bình cộng các tọa độ tương ứng của \(3\) đỉnh của tam giác.
Bài 3 trang 68 - SGK Hình học 12
Cho hình hộp \(ABCD.A'B'C'D'\) biết \(A = (1; 0; 1), B = (2; 1; 2), D = (1; -1; 1)\),
\(C' (4; 5; -5)\). Tính tọa độ các đỉnh còn lại của hình hộp.
Giải:
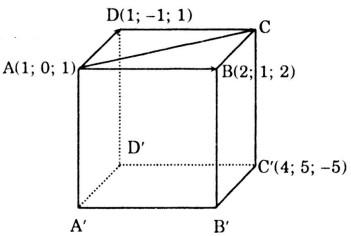
Ta có:
\(\eqalign{
& \overrightarrow {AB} = \left( {1;1;1} \right) \cr
& \overrightarrow {A{\rm{D}}} = \left( {0; - 1;0} \right) \cr
& \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \Leftrightarrow \left\{ \matrix{
{x_C} - 2 = 0 \hfill \cr
{y_C} - 1 = - 1 \hfill \cr
{z_C} - 2 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_C} = 2 \hfill \cr
{y_C} = 0 \hfill \cr
{z_C} = 2 \hfill \cr} \right. \cr} \)
Vậy \(C = (2; 0; 2)\)
Suy ra \(\overrightarrow {CC'} = \left( {2;5; - 7} \right)\)
Từ \(\overrightarrow {AA} = \overrightarrow {BB} = \overrightarrow {DD} = \overrightarrow {CC} = \left( {2;5; - 7} \right)\)
Suy ra \(\left\{ \matrix{
{x_A} - 1 = 2 \hfill \cr
{y_A} - 0 = 5 \hfill \cr
{z_A} - 1 = - 7 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
{x_A} = 3 \hfill \cr
{y_A} = 5 \hfill \cr
{z_A} = - 6 \hfill \cr} \right.\)
Vậy \(A’ (3; 5; -6)\)
Tương tự \(B’ = (4; 6; -5); D’ = (3; 4; -6)\).