Bài 1 trang 25 sgk hình học 12
Tính thể tích khối tứ diện đều cạnh \(a\).
Giải:
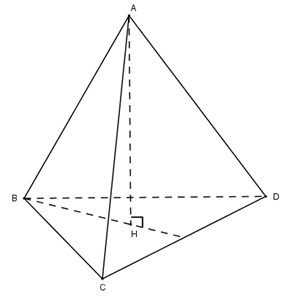
Cho tứ diện đều \(ABCD\). Hạ đường cao \(AH\) của tứ diện thì do các đường xiên \(AB, AC, AD\) bằng nhau nên các hình chiếu của chúng: \(HB, HC, HD\) bằng nhau. Do \(BCD\) là tam giác đều nên \(H\) là trọng tâm của tam giác \(BCD\).
Do đó \(BH = {2 \over 3}.{{\sqrt 3 } \over 2}a = {{\sqrt 3 } \over 3}a\)
Từ đó suy ra: \(AH^2 \)=\( a^2\)– \(BH^2 \)=\({{6{a^2}} \over 9}\)
Nên \(AH = {{\sqrt 6 } \over 3}a\)
Thể tích tứ diện đó \(V={1 \over 3} \cdot {1 \over 2} \cdot {{\sqrt 3 } \over 2}{a^2} \cdot {{\sqrt 6 } \over 3}a = {a^3}{{\sqrt 2 } \over {12}}.\)
Bài 2 trang 25 sgk hình học 12
Tính thể tích khối bát diện đều cạnh \(a\).
Giải:
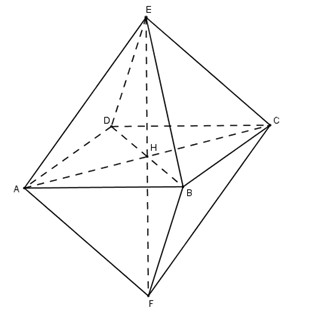
Chia khối tám mặt đều cạnh \(a\) thành hai khối chóp tứ giác đều cạnh \(a\).
Gọi \(h\) là chiều cao của khối chóp thì dễ thấy
\({h^2} = {a^2} - {\left( {{a\sqrt {2}}\over2 } \right)^2} = {{{a^2}} \over 2}\) nên \(h = {{a\sqrt 2 } \over 2}\)
Từ đó thể tích khối tám mặt đều cạnh \(a\) là:
\(V = 2.{1 \over 3}.{{\sqrt {2}}\over2}a .{a^2} = {a^3}{{\sqrt 2 } \over 3}\).
Bài 3 trang 25 sgk hình học 12
Cho hình hộp \(ABCD.A’B’C’D’\). Tính thể tích của khối hộp đó và thể tích của khối tứ diện \(ACB’D’\).
Giải:
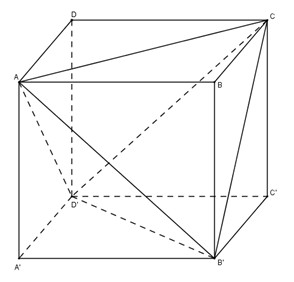
Gọi \(S\) là diện tích đáy \(ABCD\) và \(h\) là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện \(ACB’D’\) và bốn khối chóp \(A.A’B’D’, C.C’B’D’, B’.BAC\) và \(D’. DAC\). Ta thấy bốn khối chóp sau đều có diện tích đáy bằng \(\frac{S}{2}\) và chiều cao bằng \(h\), nên tổng các thể tích của chúng bằng
\(4\cdot \frac{1}{3}\cdot \frac{S}{2}h\)\(=\frac{2}{3}Sh\).
Từ đó suy ra thể tích của khối tứ diện
\(ACB’D’\)=\(\frac{1}{3}Sh\). Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện \(ACB’D’\) bằng \(3\).