Bài 5 trang 143 SGK Giải tích 12
Trong mặt phẳng tọa độ, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện:
a) phần thực của \(z\) bằng \(1\)
b) phần ảo của \(z\) bằng \(-2\)
c) Phần thực của \(z\) thuộc đoạn \([-1, 2]\), phần ảo của \(z\) thuộc đoạn \([0, 1]\)
d) \(|z| ≤ 2\)
Giải
Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có \(x = 1, y\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(x = 1\)
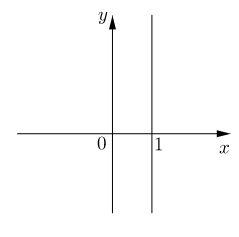
b) Ta có \(y = -2, x\) tùy ý nên tập hợp các điểm biểu diễn \(z\) là đường thẳng \(y = -2\)
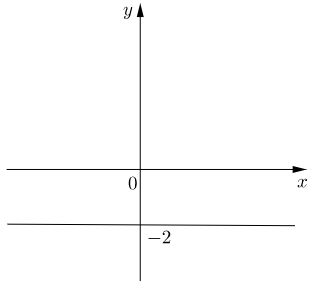
c) Ta có \(x ∈ [-1, 2]\) và \(y ∈ [0, 1]\) nên tập hợp các điểm biểu diễn \(z\) là hình chữ nhật sọc
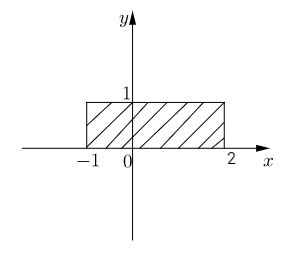
d) Ta có:
\(\left| z \right| \le 2 \Leftrightarrow \sqrt {{x^2} + {y^2}} \le 2 \Leftrightarrow {x^2} + {y^2} \le 4\)
Vậy tập hợp các điểm biểu diễn \(z\) là hình tròn tâm \(O\) (gốc tọa độ) bán kính bằng \(2\) (kể cả các điểm trên đường tròn)
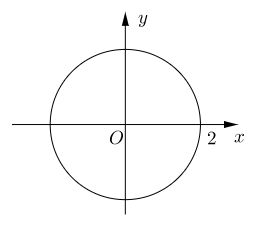
Bài 6 trang 143 SGK Giải tích 12
Tìm các số thực \(x, y\) sao cho:
a) \(3x + yi = 2y + 1 + (2-x)i\)
b) \(2x + y – 1 = (x – 2y – 5)i\)
Giải
a)
\(\eqalign{
& 3x + yi = (2y + 1)+(2 - x)i \cr
& \Leftrightarrow \left\{ \matrix{
3x = 2y + 1 \hfill \cr
y = 2 - x \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 1 \hfill \cr
y = 1 \hfill \cr} \right. \cr} \)
b)
\(\eqalign{
& 2x + y - 1 = (x + 2y - 5)i \cr
& \Leftrightarrow \left\{ \matrix{
2x + y - 1 = 0 \hfill \cr
x + 2y - 5 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = - 1 \hfill \cr
y = 3 \hfill \cr} \right. \cr} \)
Bài 7 trang 143 trang SGK Giải tích 12
Chứng tỏ rằng với mọi số phức \(z\), ta luôn có phần thực và phần ảo của \(z\) không vượt quá môdun của nó.
Giải
Giả sử \(z = a + b\)i
Khi đó: \(\left| z \right| = \sqrt {{a^2} + {b^2}}\)
Từ đó suy ra:
\(|z| \ge \sqrt {{a^2}} = |a| \ge a,|z| \ge \sqrt {{b^2}} = |b| \ge b\)
Bài 8 trang 143 SGK Giải tích 12
Thực hiện các phép tính sau:
a) \((3 + 2i)[(2 – i) + (3 – 2i)]\)
b) \((4 - 3i) + {{1 + i} \over {2 + i}}\)
c) \((1 + i)^2 – (1 – i)^2\)
d) \({{3 + i} \over {2 + i}} - {{4 - 3i} \over {2 - i}}\)
Trả lời:
a) \((3 + 2i)[(2 – i) + (3 – 2i)]= (3 + 2i)(5 – 3i) = 21 + i\)
b)
\(\eqalign{
& (4 - 3i) + {{1 + i} \over {2 + i}} = (4 - 3i) + {{(1 + i)(2 - i)} \over 5} = (4 - 3i)({3 \over 5} + {1 \over 5}i) \cr
& = (4 + {3 \over 5}) - (3 - {1 \over 5})i = {{23} \over 5} - {{14} \over 5}i \cr} \)
c) \((1 + i)^2 – (1 – i)^2 = 2i – (-2i) = 4i\)
d)
\(\eqalign{
& {{3 + i} \over {2 + i}} - {{4 - 3i} \over {2 - i}} = {{(3 + i)(2 - i)} \over 5} - {{(4 - 3i)(2 + i)} \over 5} \cr
& = {{7 - i} \over 5} - {{11 - 2i} \over 5} = {{ - 4} \over 5} + {1 \over 5}i \cr} \)