Bài 5 trang 99 SGK Hình học 12
Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \((ABC)\). Biết rằng \(AC = AD = 4 cm\), \(AB = 3 cm, BC = 5 cm\).
a) Tính thể tích tứ diện \(ABCD\).
b) Tính khoảng cách từ điểm \(A\) tới mặt phẳng \((BCD)\).
Giải
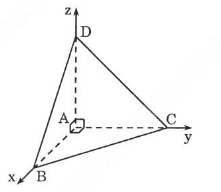
Chọn hệ toạ độ gốc là điểm \(A\), các đường thẳng \(AB, AC, AD\) theo thứ tự là các trục \(Ox, Oy, Oz\).
Ta có: \(A(0; 0; 0), B(3; 0; 0)\)
\(C(0; 4; 0), D(0; 0; 4)\)
Ta có: \(\overrightarrow {AB} = (3; 0; 0) \Rightarrow AB = 3\)
\(\overrightarrow {AC} = (0; 4; 0) \Rightarrow AC = 4\)
\(\overrightarrow {AD} = (0; 0; 4) \Rightarrow AD = 4\)
\(V_{ABCD}\) = \({1 \over 6}AB.AC.AD = 8 (cm^3)\)
b) Áp dụng công thức phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng \((BDC)\) là:
\({x \over 3} + {y \over 4} + {z \over 4} = 1 \Leftrightarrow 4x + 3y + 3z - 12 = 0\)
Từ đây ta có: \(d(A, (BDC)) ={{\left| {12} \right|} \over {\sqrt {{3^2} + {4^2} + {4^2}} }} = {{12} \over {\sqrt {34} }}\)
Bài 6 trang 100 SGK Hình học 12
Trong không gian \(Oxyz\) cho mặt cầu \((S)\) có phương trình \({x^2} + {\rm{ }}{y^2} + {\rm{ }}{z^2} = {\rm{ }}4{a^{2}}\left( {a > 0} \right)\).
a) Tính diện tích mặt cầu \((S)\) và thể tích của khối cầu tương ứng.
b) Mặt cầu \((S)\) cắt mặt phẳng \((Oxy)\) theo đường tròn \((C)\). Xác định tâm và bán kính của \((C)\).
c) Tính diện tích xung quanh của hình trụ nhận \((C)\) làm đáy và có chiều cao là \(a\sqrt3\). Tính thể tích của khối trụ tương ứng.
Giải
a) Mặt cầu \((S)\) có tâm là gốc toạ độ \(O\) và bán kính \(R = 2a\) nên có
\(S = 16πa^2\) ; \(V ={{32\pi {a^2}} \over 3}\)
b) Phương trình đường tròn \((C)\), giao tuyến của mặt cầu và mặt phẳng \(Oxy\) là:\(\left\{ \matrix{
{x^2} + {y^2} + {z^2} = 4{a^2} \hfill \cr
z = 0 \hfill \cr} \right.\)
Từ đây suy ra mặt phẳng \(z = 0\) cắt mặt cầu theo đường tròn \((C)\) có tâm là gốc toạ độ \(O\) và bán kính là \(2a\).
c) Hình trụ có đáy là đường tròn \((C)\) và chiều cao \(a\sqrt3\) có:
\(S_{xq} = 2π.(2a).a\sqrt3\) \( \Rightarrow S_{xq}= 4πa^2\sqrt3\)
\(V = π(2a)^2.a\sqrt3\) \( \Rightarrow V = 4πa^3\sqrt3\)
Bài 7 trang 100 SGK Hình học 12
Trong không gian \(Oxyz\) cho hai đường thẳng d1 và d2 có phương trình
d1:\(\left\{ \matrix{
x = 1 - t \hfill \cr
y = t \hfill \cr
z = - t \hfill \cr} \right.\) và d2:\(\left\{ \matrix{
x = 2k \hfill \cr
y = - 1 + k \hfill \cr
z = k. \hfill \cr} \right.\)
a) Chứng minh rằng hai đường thẳng d1 và d2 chéo nhau.
b) Viết phương trình mặt phẳng \((α)\) chứa d1 và song song với d2.
Giải
a) (d1) đi qua điểm \(M(1; 0; 0)\) và có vectơ chỉ phương \(\overrightarrow a = (-1; 1; -1)\)
(d2) đi qua điểm \(M'(0; -1; 0)\) và có vectơ chỉ phương \(\overrightarrow {a'} = (2; 1; 1)\)
Vì \(\overrightarrow a \) và \(\overrightarrow {a'} \) không cùng phương nên d1 và d2 có thể chéo nhau hoặc cắt nhau. Xét giao của d1 và d2:\(\left\{ \matrix{
1 - t = 2k \hfill \cr
t = - 1 + k \hfill \cr
- 1 = k \hfill \cr} \right.\), hệ vô nghiệm
do đó d1 và d2 không cắt nhau. Từ đó suy ra d1 và d2 chéo nhau.
b) Mặt phẳng \((α)\) chứa (d1) và song song với d2 thì \((α)\) qua điểm \(M_1(1; 0; 0)\) và có vectơ pháp tuyến \(\overrightarrow n = \left[ {\overrightarrow {{a_1}} ,\overrightarrow {{a_2}} } \right]= (2; -1; -3)\)
Phương trình mặt phẳng \((α)\) có dạng:
\(2(x - 1) - (y - 0) - 3(z - 0) = 0\)
hay \(2x - y - 3z - 2 = 0\)
Bài 8 trang 100 SGK Hình học 12
Trong không gian \(Oxyz\) cho các điểm \(A(1; 0 ; -1), B(3 ; 4 ; -2), C(4 ; -1; 1), D(3 ; 0 ;3)\).
a) Chứng minh rằng \(A, B, C, D\) không đồng phẳng.
b) Viết phương trình mặt phẳng \((ABC)\) và tính khoảng cách từ \(D\) đến \((ABC)\).
c) Viết phương trình mặt cầu ngoại tiếp tứ diện \(ABCD\).
d) Tính thể tích tứ diện \(ABCD\).
Giải
a) Ta có: \(\overrightarrow {AB} = (2; 4; 3)\).
Phương trình tham số của đường thẳng \(AB\):
\(\left\{ \matrix{
x = 1 + 2t \hfill \cr
y = 4t \hfill \cr
z = - 1 + 3t \hfill \cr} \right.\)
\(\overrightarrow {CD} = (-1; 1; 2)\). Phương trình tham số của \(CD\):
\(\left\{ \matrix{
x = 4 - k \hfill \cr
y = - 1 + k \hfill \cr
z = 1 + 2k \hfill \cr} \right.\)
Do \(\overrightarrow {AB} \ne k\overrightarrow {CD} \) nên hai đường thẳng \(AB, CD\) không cùng phương, chúng cắt nhau hoặc chéo nhau.
Xét hệ:
\(\left\{ \matrix{
1 + 3t = 4 - t'(1) \hfill \cr
4t = - 1 + t'(2) \hfill \cr
- 1 + 3t = 1 + 2t'(3) \hfill \cr} \right.\)
Từ hai phương trình đầu, ta có: \(t = {2 \over 7}\); \(t' = {{15} \over 7}\)
Hai giá trị này không thoả mãn phương trình (3) nên hệ vô nghiệm, suy ra \(AB\) và \(CD\) không cắt nhau.
Vậy \(AB\) và \(CD\) là hai đường thẳng chéo nhau hay bốn điểm \(A, B, C, D\) không đồng phẳng.
b) Ta có \(\overrightarrow {AB} = (2; 4; -1)\), \(\overrightarrow {AC} = (3; -1; 2)\)
Gọi \(\overrightarrow n \) là vectơ pháp tuyến của mặt phẳng \((ABC)\)
\(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (7; -7; -14)\)
phương trình mp \((ABC)\): \(7(x - 1) - 7(y - 0) -14(z + 1) = 0\)
\(7x - 7y -14z - 21 = 0 \Leftrightarrow x - y - 2z - 3 = 0\).
\(d(D, (ABC))\) =\({{\left| {1.3 - 0 - 2.3 - 3} \right|} \over {\sqrt {{1^2} + {1^2} + {{( - 2)}^2}} }} = {6 \over {\sqrt 6 }} = \sqrt 6 \)
c) Phương trình tổng quát của mặt cầu:
\({x^2} + {y^2} + {z^2} + 2Ax + 2By + 2Cz + D = 0\)
Mặt cầu đi qua \(A(1; 0; -1)\) ta có:
\({1^2} + {0^2} + {( - 1)^2} + 2A - 2C + D = 0\)
\( \Leftrightarrow 2A - 2C + D + 2 = 0 \) (1)
Tương tự, mặt cầu đi qua \(B, C, D\) cho ta các phương trình:
\(2A + 8B - 2C + D + 18 = 0 \) (2)
\(4A + 8B + 6C + D + 29 = 0 \) (3)
\(4A + 4B - 2C + D + 9 = 0 \) (4)
Hệ bốn phương trình (1), (2), (3), (4) cho ta: \(A = 3; B = 2; C = {1 \over 2}; D = 3\). Ta được tâm của mặt cầu \(I\)\(\left( { - 3; - 2; - {1 \over 2}} \right)\) và bán kính:
\(R = 3^2+ 2^2 + {\left( {{1 \over 2}} \right)^2} - 3 = {{41} \over 4} \Rightarrow R = {{\sqrt {41} } \over 2}\)
Phương trình mặt cầu đi qua bốn điểm \(A, B, C, D\) là:
\((x - 3)^2 + (y - 2)^2 + {\left( {z - {1 \over 2}} \right)^2} = {{41} \over 4}\)
d) Ta có \(\overrightarrow {AB} = (2; 4; -1)\) \( \Rightarrow AB^2= 4 + 16 + 1 = 21\)\( \Rightarrow AB = \sqrt {21} \)
\(\overrightarrow {AC} = (3; -1; 2)\) \( \Rightarrow AC^2 = 9 + 1 + 4 = 14\)\( \Rightarrow AC = \sqrt {14} \)
Xét \(\overrightarrow {AB} .\overrightarrow {AC} = 2.3 + 4.(-1) + (-1).2 = 0\)\( \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AC} \)
Tam giác \(ABC\) vuông tại đỉnh \(A\), có diện tích:
\({S_{ABC}} = {1 \over 2}AB.AC = {1 \over 2}\sqrt {21} .\sqrt {14} \)
Thể tích tứ diện \(ABCD\):
\({V_{ABCD}} = {1 \over 3}.{S_{ABC}}.DH = {1 \over 3}.{1 \over 2}.\sqrt {21} .\sqrt {14} .\sqrt 6 = 7\) (Đvdt)