Bài 1 trang 60 sgk giải tích 12
Tìm tập xác định của các hàm số:
a) y= \(\left ( 1-x \right )^{\frac{-1}{3}}\);
b) y= \(\left ( 2-x^{2} \right )^{\frac{3}{5}}\);
c) y= \(\left ( x^{2}-1 \right )^{-2}\);
d) y= \(\left ( x^{2}-x-2\right )^{\sqrt{2}}\).
Giải
a) \(y= \left ( 1-x \right )^{\frac{-1}{3}}\) xác định khi \(1-x > 0 ⇔ x< 1\). Tập xác định là \((-∞; 1)\).
b) \(y= \left ( 2-x^{2} \right )^{\frac{3}{5}}\) xác định khi \(2-x^2> 0 ⇔ \)
-\(\sqrt{2} < x <\) \(\sqrt{2}\).
Tập xác định là (-\(\sqrt{2}\); \(\sqrt{2}\)).
c) \(y= \left ( x^{2}-1 \right )^{-2}\) xác định khi \(x^2-1\ne 0 ⇔ x \ne ± 1\).
Tập xác định là \(\mathbb R {\rm{\backslash }} {\rm{\{ - 1;1\} }}\) .
d) \(y= \left ( x^{2}-x-2\right )^{\sqrt{2}}\) xác định khi \(x^2-x-2 > 0 ⇔ x <-1;x > 2\).
Tập xác định là: \((-∞;-1) ∪ (2; +∞)\).
Bài 2 trang 61 sgk giải tích 12
Tìm các đạo hàm của các hàm số:
a) \(y= \left ( 2x^{2} -x+1\right )^{\frac{1}{3}}\);
b) \(y= \left ( 4-x-x^{2}\right )^{\frac{1}{4}}\);
c) \(y= \left ( 3x+1\right )^{\frac{\pi }{2}}\);
d) \(y= \left ( 5-x\right )^{\sqrt{3}}\).
Giải
a) \(y^{'}=\frac{1}{3}\left ( 2x^{2} -x+1\right )^{'}\left (2x^{2}-x+1 \right )^{\frac{1}{3}-1}\)= \(\frac{\left ( 4x-1\right )\left ( 2x^{2}-x+1 \right )^{\frac{-2}{3}}}{3}\).
b) \(y^{'}=\frac{1}{4}\left ( 4-x-x^{2} \right )^{'}\left ( 4-x-x^{2} \right )^{\frac{1}{4}-1}\)= \(\frac{1}{4}\left ( -2x-1 \right )\left ( 4-x-x^{2} \right )^{\frac{-3}{4}}\).
c) \(y^{'}\)= \(\frac{\pi }{2}\left ( 3x+1 \right )^{'}\left ( 3x+1 \right )^{\frac{\pi }{2}-1}\)= \(\frac{3\pi }{2}\left ( 3x+1 \right )^{\frac{\pi }{2}-1}\).
d) \(y^{'}\)= \(\sqrt{3}\left ( 5-x \right )^{'}\left ( 5-x \right )^{\sqrt{3}-1}\)= \(-\sqrt{3}\left ( 5-x \right )^{\sqrt{3}-1}\).
Bài 3 trang 61 sgk giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
a) \(y=x^{4\over3}\) ;
b) \(y=x^{-3}\).
Giải
a) Hàm số \(y=x^{4\over3}\)
Tập xác định: \(\mathbb R\).
Sự biến thiên:
\(y' = {4 \over 3}{x^{{1 \over 3}}} \)
- Hàm số nghịch biến trên khoảng \((-\infty;0)\), đồng biến trên khoảng \((0;+\infty)\)
- Giới hạn đặc biệt:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \).
- Đồ thị hàm số không có tiệm cận.
- Bảng biến thiên
.png)
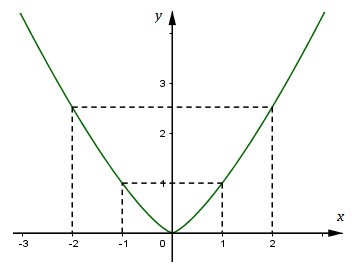
Đồ thị( hình bên). Đồ thị hàm số qua \((1;1)\), \((2;\root 3 \of {{2^4}} )\).
b) \(y = {x^{ - 3}}\)
Tập xác định: \(D=\mathbb ℝ \backslash {\rm{\{ }}0\} \).
Sự biến thiên:
\(y' = - 3{x^{ - 4}} < 0,\forall x \in D\)
- Hàm nghich biến trong khoảng \((-∞;0)\) và \((0; +∞)\).
- Giới hạn đặc biệt:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} y = + \infty \cr
& \mathop {\lim }\limits_{x \to {0^ - }} y = - \infty \cr
& \mathop {\lim }\limits_{x \to \pm \infty } y = 0 \cr }\)
- Đồ thị hàm số nhận trục tung làm tiệm cận đứng, trục hoành làm tiệm cận ngang.
- Bảng biến thiên
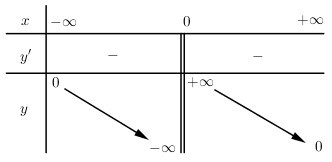
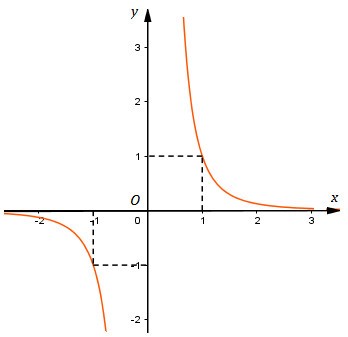
Đồ thị qua \((-1;-1)\), \((1;1)\), \(\left( {2;{1 \over 8}} \right)\), \(\left( {-2;{-1 \over 8}} \right)\). Hàm số đồ thị đã cho là hàm số lẻ nên đối xứng qua gốc tọa độ.