Bài 8 trang 40 sách giáo khoa hình học lớp 12
Một hình trụ có hai đáy là hai hình tròn \((O;r)\) và \((O';r)\). Khoảng cách giữa hai đáy là \(OO' = r.\sqrt3\). Một hình nón có đỉnh là \(O'\) và có đáy là hình tròn \((O;r)\).
a) Gọi \(S_1\) là diện tích xung quanh của hình trụ và \(S_2\) là diện tích xung quanh của hình nón, hãy tính tỷ số \({{{S_1}} \over {{S_2}}}\).
b) Mặt xung quanh của hình nónchia khối trụ thành hai phần, hãy tính tỷ số thể tích hai phần đó.
Giải:
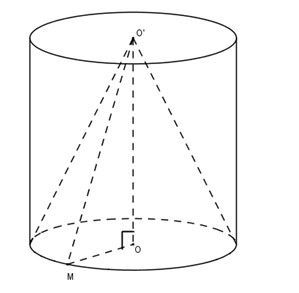
Ta có \(l = h = r\sqrt3\)
Diện tích xung quanh hình trụ là:
\(S_1 = 2πr.l = 2πr.r\sqrt3 = 2\sqrt3 πr^2\)
\(O'M\) là một đường sinh của hình nón ta có:
\(l' = O'M = \sqrt {OO{'^2} + O{M^2}} = \sqrt {3{r^2} + {r^2}} = 2r\)
Diện tích xung quanh hình nón là:
\(S_2 = πrl'= π.r.2r = 2πr^2\)
Vậy: \({{{S_1}} \over {{S_2}}} = {{2\sqrt 3 \pi {r^2}} \over {2\pi {r^2}}} = \sqrt 3 \)
b) Khối trụ và khối nón có cùng đáy và cùng chiều cao nên thể tích khối trụ bằng ba lần thể tích khối nón. Gọi \(V_1\) là thể tích khối nón và \(V_3\) là thể tích phần còn lại của khối trụ, ta suy ra: \({{{V_1}} \over {{V_2}}} = {1 \over 2}\)
Bài 9 trang 40 sách giáo khoa hình học lớp 12
Cắt hình nón đỉnh \(S\) bởi mặt phẳng đi qua trục ta được một tam giác vuông cân có cạnh huyền bằng \(a\sqrt2\).
a) Tính diện tích xuang quanh, diện tích đáy và thể tích của khối nón tương ứng.
b) Cho một dây cung \(BC\) và đường tròn đáy hình nón sao cho mặt phẳng \((SBC)\) tạo với mặt phẳng chứa đáy hình nón một góc \(60^0\). Tính diện tích hình vuông và mặt phẳng đáy.
Giải:
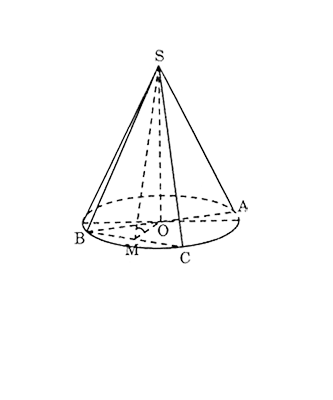
a) Cạnh huyền chính bằng đường kính đáy do vậy bán kính đáy \(r = \frac{a\sqrt{2}}{2}\) và đường cao \(h = r\), đường sinh \(l = a\).
Vậy \(S_xq = πrl =\) \( \frac{\sqrt{2}}{2}\pi a^2\) ( đơn vị diện tích)
\(S\)đáy = \( \pi r^{2}\) = \( \pi \frac{a^{2}}{2}\) ( đơn vị diện tích);
\(V\)nón = \( \frac{1}{3}\pi r^{2}h\) \( = \frac{\sqrt{2}}{12}\pi a^{3}\) ( đơn vị thể tích)
b) Gọi tâm đáy là \(O\) và trung điểm cạnh \(BC\) là \(M\).
Theo giả thiết, \( \widehat{SMO}\) = \(60^0\).
Ta có diện tích \(∆ SBC\) là: \(S = {{SM.BC}\over2}\)
Ta có \(SO = SM.sin60^0\) = \( \frac{\sqrt{3}}{2}SM\).
Vậy \( SM = \frac{2}{\sqrt{3}}SO = \frac{\sqrt{6}}{3}a\).
Ta có \(∆ OMB\) vuông ở \(M\) và \(BO = r\) = \( \frac{a\sqrt{2}}{2}\);
\(OM = SM.cos60^0\) = \( \frac{\sqrt{6}}{6}a\).
\( BM^{2}= BO^{2} - OM^{2} = \frac{a^{2}}{3}\)
Vậy \(BM\) = \( \frac{a}{\sqrt{3}}\) và \(BC\) = \( \frac{2a}{\sqrt{3}}\).
Do đó \(S = {{SM.BC}\over2}\) = \( \frac{\sqrt{2}}{3}a^{2}\) (đơn vị diện tích)
Bài 10 trang 40 sách giáo khoa hình học lớp 12
Cho hình trụ có bán kính \(r\) và có chiều cao cũng bằng \(r\). Một hình vuông \(ABCD\) có hai cạnh \(AB\) và \(CD\) lần lượt là các dây cung của hai đường tròn đáy, còn cạnh \(BC\) và \(AD\) không phải là đường sinh của hình trụ. Tính diện tích của hình vuông đó và cosin của góc giữa mặt phẳng chứa hình vuông và mặt phẳng đáy.
Giải:
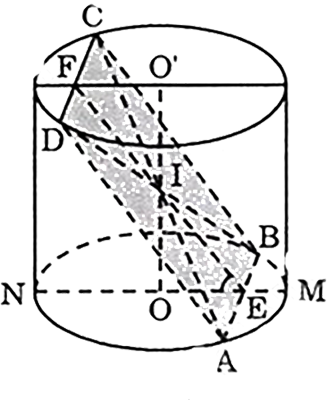
Do tính chất đối xứng của \((ABCD)\) nên \((ABCD)\) cắt \(OO'\) tại trung điểm \(I\) của \(OO'\). \(I\) cũng là giao điểm của hai đường chéo \(AC,BD\).
Xét tam giác vuông \(IOB\) ta có:
\(IB^2=IO^2+OB^2\)
\(\Rightarrow IB=\sqrt {{{\left( {{r \over 2}} \right)}^2} + {r^2}} = {{r\sqrt 5 } \over 2}\)
\(\Rightarrow AC=BD=2IB=r\sqrt5; AB={{r\sqrt {10} } \over 2}\).
Suy ra: \(S_{ABCD}={{5{r^2}} \over 2}\).
Gọi \(E\) là trung điểm của \(AB\)
\(\Rightarrow DE\bot AB, IE\bot AB\).
\(\Rightarrow \widehat {IEO}\) là góc giữa \((ABCD)\) và mặt đáy của hình trụ.
\(IE = {{r\sqrt {10} } \over 4}, OI={r\over 2}\)
\(sin\widehat {IEO}={{OI}\over {IE}}={\sqrt{10}\over5}\)