Bài 8 trang 49 sách giáo khoa hình học lớp 12
Chứng minh rắng nếu có một mặt cầu tiếp xúc với \(6\) cạnh của một hình tứ diện thì tổng độ dài của các cặp cạnh đối diện tứ diện bằng nhau.
Giải:
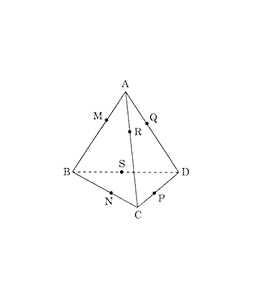
Giả sử tứ diện \(ABCD\) có mặt cầu tiếp xúc với cả \(6\) cạnh của tứ diện; tiếp xúc với \(AB, BC, CD,AD,AC,BD\) lần lượt tại \(M,N,P,Q,R,S\). Vì các đoạn thẳng kẻ từ một điểm đến tiếp điểm của các tiếp tuyến đó bằng nhau, nên ta có:
\( \left\{\begin{matrix} AM= AR = AQ\\ BM= BN= BS\\ CN= CP= CR\\ DP = DQ = DS\\ \end{matrix}\right.\)
Ta chứng minh: \(AB + CD = AC +BD = AD + BC\).
Ta có
\(AM + MB + CP + PD \)\(=AR+RC+BS+SD\)
\(= AQ + QD + BN + NC\)
Hay: \(AB + CD = AC +BD = AD + BC\).
Bài 9 trang 49 sách giáo khoa hình học lớp 12
Cho một điểm \(A\) cố định và một đường thẳng \(a\) cố định không đi qua \(A\). Gọi \(O\) là một điểm thay đổi trên \(a\). Chứng minh rằng các mặt cầu tâm \(O\) và bán kính \(r = OA\) luôn luôn đi qua một đường tròn cố định.
Giải:
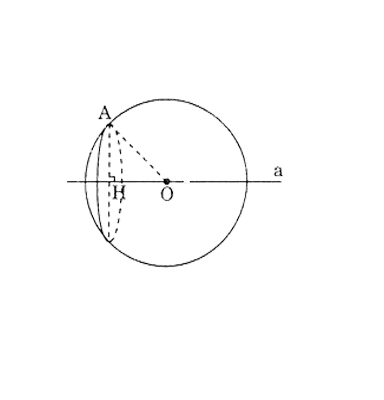
Xét mặt phẳng \((P)\) qua điểm \(A\) và \((P)\) vuông góc với đường thẳng \(a\). Goi giao của \((P)\) với \(a\) là điểm \(H\). Xét mặt cầu tâm \(O\) bán kính \(r = OA\); mặt cầu này giao với mặt phẳng \((P)\) theo đường tròn tâm \(H\) là hình chiếu vuông góc của \(O\) lên \((P)\) và bán kính \(HA \) cố định.
Bài 10 trang 49 sách giáo khoa hình học lớp 12
Cho hình chóp \(S.ABC\) có bốn đỉnh đếu nằm trên một mặt cầu, \(SA = a, SB = b, SC = c\) và ba cạnh \(SA, SB, SC\) đôi một vuông góc. Tính diện tích mặt cầu và thể tích khối cầu được tạo bởi mặt cầu đó
Giải:
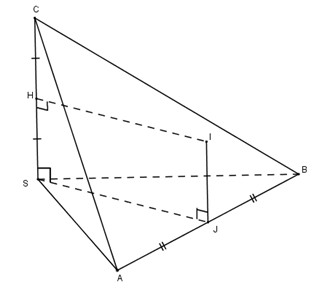
Gọi \(I\) là tâm cầu ngoại tiếp hình chóp tam giác \(S.ABC\). Hạ \(IJ\) vuông góc \((SAB)\), vì \(J\) cách đều \(3\) điểm \(S, A, B\) nên \(J\) cũng cách đều \(3\) điểm \(S, A, B\).
Vì tam giác \(SAB\) vuông đỉnh \(S\) nên \(J\) là trung điểm của \(AB\).
Ta có \(SJ ={1 \over 2}AB = {1 \over 2}\sqrt {{a^2} + {b^2}}\)
Do \(SC\) vuông góc \((SAB)\) nên \(IJ // SC\).
Gọi \(H\) là trung điểm \(SC\), ta có \(SH = IJ = {c \over 2}\).
Do vậy, \(I{S^2} = I{J^2} + S{J^2} = {{({a^2} + {b^2} + {c^2})} \over 4}\) và bán kính hình cầu ngoại tiếp \(S.ABC\) là
\(r = IS = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Diện tích mặt cầu là:
\(S = 4\pi {r^2} = \pi ({a^2} + {b^2} + {c^2})\)
\(V = {4 \over 3}\pi {r^3} = {1 \over 6}\pi {\left( {{a^2} + {b^2} + {c^2}} \right)^{{3 \over 2}}}\).