Bài 1 trang 9 sách sgk giải tích 12
Xét sự đồng biến, nghịch biến của các hàm số:
a) \(y = 4 + 3x - x^2\) ; b) \(y ={1 \over 3}x^3\) + \(3x^2-7x - 2\) ;
c) \(y = x^4\) - \(2x^2\) +\( 3\) ; d) \(y = -x^3\)+ \(x^2\) - \(5\).
Giải:
1. a) Tập xác định : \(D =\mathbb R\);
\(y' = 3 - 2x => y' = 0 ⇔ x =\) \({3 \over 2}\).
Bảng biến thiên :
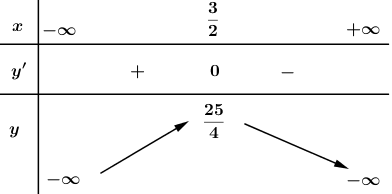
Hàm số đồng biến trên khoảng \(\left( { - \infty ;{3 \over 2}} \right)\); nghịch biến trên khoảng \(\left( { {3 \over 2}};+\infty \right)\)
b) Tập xác định \(D=\mathbb R\);
\(y'= x^2\)+ \(6x - 7 \Rightarrow y' = 0 ⇔ x = 1, x = -7\).
Bảng biến thiên :
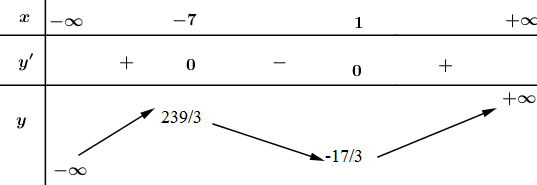
Hàm số đồng biến trên các khoảng \((-∞ ; -7), (1 ; +∞)\) ; nghịch biến trên các khoảng \((-7 ; 1)\).
c) Tập xác định : \(D=\mathbb R\).
\(y' = 4x^3\)-\(4x = 4x(x^2-1)\) \(\Rightarrow y' = 0 ⇔ x = -1, x = 0, x = 1\).
Bảng biến thiên :
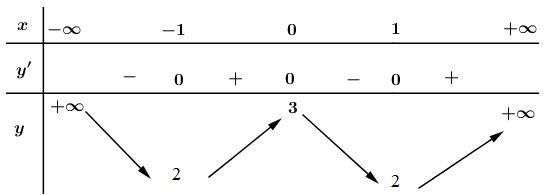
Hàm số đồng biến trên các khoảng \((-1 ; 0), (1 ; +∞)\) ; nghịch biến trên các khoảng \((-∞ ; -1), (0 ; 1)\).
d) Tập xác định :\( D=\mathbb R\).
\(y' = -3x^2\) +\( 2x \Rightarrow y' = 0 ⇔ x = 0, x =\) \({2 \over 3}\).
Bảng biến thiên :
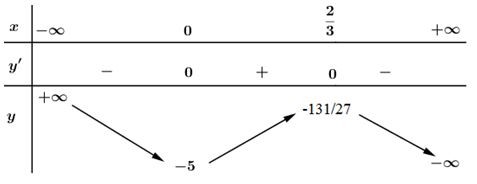
Hàm số đồng biến trên khoảng \(( 0 ; {2 \over 3} )\) ; nghịch biến trên các khoảng \((-∞ ; 0)\), \(({2 \over 3}; +∞)\).
Bài 2 trang 10 sách sgk giải tích 12
Tìm các khoảng đơn điệu của các hàm số:
a) \(y=\frac{3x+1}{1-x}\) ; b) \(y=\frac{x^{2}-2x}{1-x}\) ;
c) \(y=\sqrt{x^{2}-x-20}\) ; d) \(y=\frac{2x}{x^{2}-9}\).
Giải
a) Tập xác định : \(D =\mathbb R \setminus\){ 1 }.
\(y'=\frac{4}{(1-x)^{2}}\)> 0, \(∀x \neq 1\).
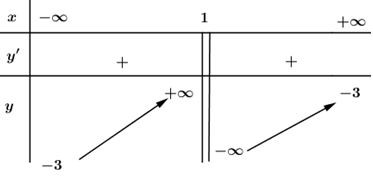
Hàm số đồng biến trên các khoảng : \((-∞ ; 1), (1 ; +∞)\).
b) Tập xác định : \(D =\mathbb R\setminus\){ 1 }.
\(y'=\frac{-x^{2}+2x-2}{(1-x)^{2}}< 0\), \(∀x \neq 1\).
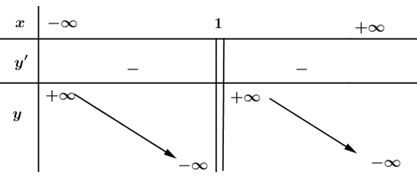
Hàm số nghịch biến trên các khoảng: \( (-∞ ; 1), (1 ; +∞)\).
c) Tập xác định :\( D = (-∞ ; -4] ∪ [5 ; +∞)\).
\(y'=\frac{2x-1}{2\sqrt{x^{2}-x-20}}\) \(∀x ∈ (-∞ ; -4] ∪ [5 ; +∞)\).
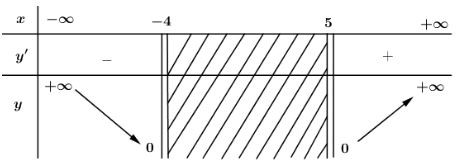
Với \(x ∈ (-∞ ; -4)\) thì \(y’ < 0\); với \(x ∈ (5 ; +∞)\) thì \(y’ > 0\). Vậy hàm số nghịch biến trên khoảng \((-∞ ; -4)\) và đồng biến trên khoảng \((5 ; +∞)\).
d) Tập xác định : \(D =\mathbb R\setminus \){ -3 ; 3 }.
\(y'=\frac{-2(x^{2}+9)}{\left (x^{2}-9 \right )^{2}} < 0, ∀x \neq ±3\).
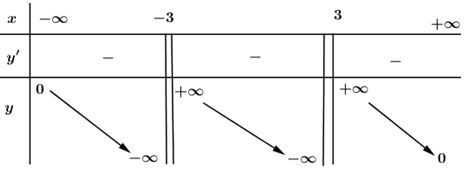
Hàm số nghịch biến trên các khoảng : \((-∞ ; -3), (-3 ; 3), (3 ; +∞)\).
Bài 3 trang 10 sách sgk giải tích 12
Chứng minh rằng hàm số \(y={{1 - {x^2}} \over {{{({x^2} + 1)}^2}}}\) đồng biến trên khoảng \((-1 ; 1)\) và nghịch biến trên các khoảng \(( - \infty ; - 1)\) và \((1 ; +∞)\).
Giải:
Tập xác định : \(D=\mathbb R\).
\(y' = {{1 - {x^2}} \over {{{({x^2} + 1)}^2}}}\) \(\Rightarrow y' = 0 ⇔ x=-1\) hoặc \(x=1\).
Bảng biến thiên :
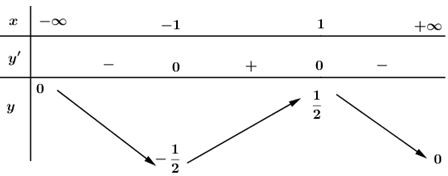
Vậy hàm số đồng biến trên khoảng \((-1 ; 1)\); nghịch biến trên các khoảng \((-∞ ; -1), (1 ; +∞)\).