Bài 5 trang 49 sách giáo khoa hình học lớp 12
Từ một điểm \(M\) nằm nằm bên ngoài mặt cầu \(S( O; r)\) ta kẻ hai đường thẳng cắt mặt cầu lần lượt tại \(A, B\) và \(C, D\).
a) Chứng minh rằng \(MA.MB = MC.MD\).
b) Gọi \(MO = d\). Tính \(MA.MB\) theo \(r\) và \(d\).
Giải:
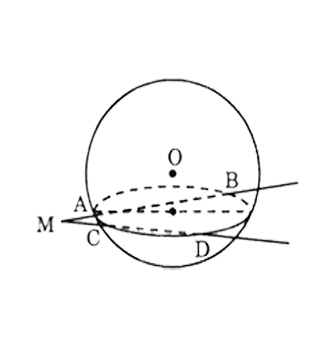
a) Gọi \((P)\) là mặt phẳng chứa hai đường thẳng đã cho. Mặt phẳng\((P)\) cắt mặt cầu \(S(O;r)\) theo một đường tròn tâm \(I\), là hình chiếu vuông góc của \(O\) lên mặt phẳng \((P)\).
Xét hai tam giác \(MAD\) và \(MCB\) có:
+) \(\widehat B = \widehat D\) (Hai góc cùng chắn một cung)
+) \(\widehat M\)
\( \Rightarrow \Delta MAD\) đồng dạng \(\Delta MCB\).
\(\Rightarrow{{MA} \over {MC}} = {{MD} \over {MB}}\Rightarrow MA.MB=MC.MD\)
b) Đặt \(MO = d\), ta có \(OI\) vuông góc với \((P)\) và ta có:
\(O{M^2} = M{I^2} = O{I^2};O{A^2} = O{I^2} + I{A^2}\)
Hạ \(IH\) vuông góc \(AB\), ta có \(H\) là trung điểm của \(AB\).
Ta có \(MA = MH - HA\); \(MB = MH + HB = MH + HA\).
\(MA.MB = M{H^2} - H{A^2}\)
\(\eqalign{
& = (M{H^2} + H{I^2}) - (H{A^2} + I{H^2}) \cr
& = M{I^2} - I{A^2} \cr
& = (M{I^2} + O{I^2}) - (I{A^2} + O{I^2}) \cr
& = O{M^2} - O{A^2} \cr
& = {d^2} - {r^2} \cr} \)
Vậy \(MA.MB = {d^2} - {r^2}\).
Bài 6 trang 49 sách giáo khoa hình học lớp 12
Gọi mặt cầu \(S(O; r)\) tiếp xúc với \((P)\) tại \(I\). Gọi \(M\) là một điểm nằm trên mặt cầu nhưng không phải là điểm đối xứng với \(I\) qua tâm \(O\). Từ \(M\) kẻ hai tiếp tuyến cắt của mặt cầu cắt \((P)\) tại \(A\) và \(B\). Chứng minh rằng \( \widehat{AMB}= \widehat{AIB}\).
Giải:
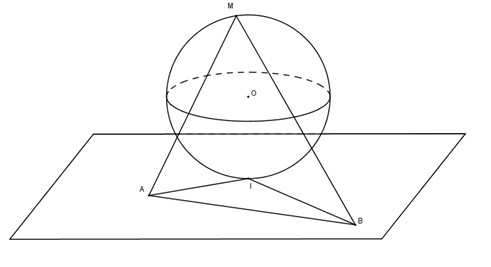
Theo tính chất của mặt cầu, ta có \(AI\) và \(AM\) là hai tiếp tuyến với cầu kẻ từ \(A\), cho nên \(AI = AM\), tương tự \(BI =BM\).
Hai tam giác \(ABI\) và \(ABM\) bằng nhau (c.c.c)
\( \Rightarrow \widehat{AMB}= \widehat{AIB}\) (Hai góc tương ứng).
Bài 7 trang 49 sách giáo khoa hình học lớp 12
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AA' = a, AB = b, AD = c\).
a) Hãy xác định tâm và bán kính của mặt cầu đi qua 8 đỉnh của hình hộp đó.
b) Tính bán kính của đường tròn là giao tuyến của mặt phẳng \((ABCD)\) với mặt cầu trên.
Giải:
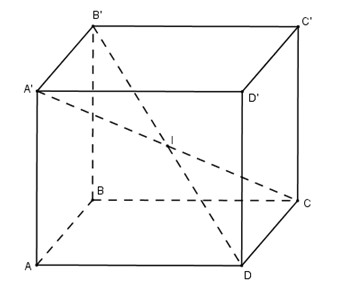
a) Trong hình hộp chữ nhật, bốn đường chéo \(AC', BD', CA' và DB'\) cắt nhau tại điểm \(I\) là trung điểm của mỗi đường.
Vì \(4\) đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm \(I\) cách đều \(8\) đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.
Vì \(AB = b, AD = c, AA' = a\) nên bán kính mặt cầu \(R = {1 \over 2}A'C = {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \).
b) Giao tuyến của mặt phẳng\(( ABCD)\) với mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.A'B'C'D'\) là đường tròn ngoại tiếp hình chữ nhật \(ABCD\). Nên bán kính của đường trong giao tuyến là:
\(r = {1 \over 2}AC = {1 \over 2}\sqrt {{b^2} + {c^2}} \)