Bài 4 trang 24 sách sgk giải tích 12
Tính giá trị lớn nhất của các hàm số sau:
a) \(y = {4 \over {1 + {x^2}}}\); b) \(y = 4{x^3} - 3{x^4}\)
Giải:
a) Tập xác định \(D=\mathbb R\).
\(y' = - {{8x} \over {{{(1 + {x^2})}^2}}}\); \(y' = 0 \Leftrightarrow x = 0\)
\(\mathop {\lim y}\limits_{x \to \pm \infty } = 0\).
Ta có bảng biến thiên :
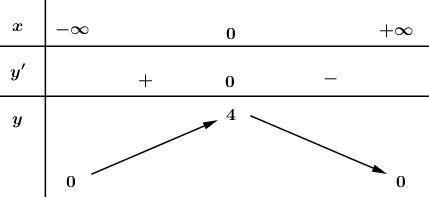
Từ bảng biến thiên ta thấy \(max\) \(y = 4\) .
b) Tập xác định \(D=\mathbb R\).
\(y{\rm{ }} = {\rm{ }}12{x^2}-{\rm{ }}12{x^3} = {\rm{ }}12{x^2}\left( {1{\rm{ }}-{\rm{ }}x} \right)\) ;
\(y’ = 0 ⇔ x = 0, x = 1\) ;\(\mathop {\lim y}\limits_{x \to \pm \infty } = - \infty \).
Ta có bảng biến thiên :
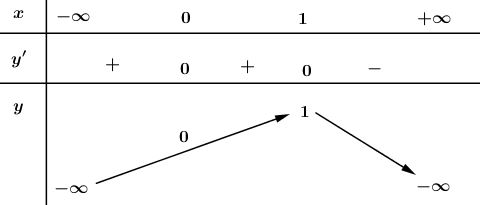
Từ bảng biến thiên ta thấy \(max\) \(y=1\).
Bài 5 trang 24 sách sgk giải tích 12
Tính giá trị nhỏ nhất của các hàm số sau:
a) \(y =|x|\) ; b) \(y =x+{4\over x}\) \(( x > 0)\).
Giải:
a)
\(y = |x| = \left\{ \matrix{
x,x \ge 0 \hfill \cr
- x,x < 0 \hfill \cr} \right.\)
Tập xác định \(D =\mathbb R\). Ta biết rằng hàm số liên tục tại \(x = 0\) nhưng không có đạo hàm tại điểm này. Ta có bảng biến thiên :
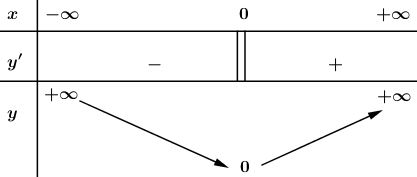
Từ bảng biến thiên ta thấy \(min\) \(y=0\).
b) Tập xác định \(D = (0 ; +∞ )\).
\(y' = 1 - {4 \over {{x^2}}} = {{{x^2} - 4} \over {{x^2}}}\); \(y' = 0 ⇔ x = 2\) (do \(x > 0\));
Ta có bảng biến thiên :
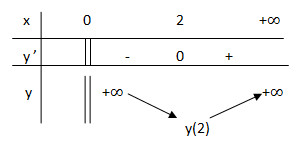
Từ bảng biến thiên ta thấy \(\min\) \(y= 4\).