Bài 5 trang 45 SGK Giải tích 12
Cho hàm số \(y = 2x^2 + 2mx + m -1\) có đồ thị là (Cm), \(m\) là tham số
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi \(m = 1\)
b) Xác định m để hàm số:
- Đồng biến trên khoảng \((-1, +∞)\)
- Có cực trị trên khoảng \((-1, +∞)\)
c) Chứng minh rằng (Cm) luôn cắt trục hoành tại hai điểm phân biệt với mọi \(m\).
Giải
\(y = 2x^2 + 2mx + m -1\) (Cm). Đây là hàm số bậc hai, đồ thị là parabol quay bề lõm lên phía trên.
a) \(m = 1 ⇒ y = 2x^2+ 2x\)
Tập xác định \(D =\mathbb R\)
* Sự biến thiên:
\(y' = 4x + 2 = 0 \Leftrightarrow x = {{ - 1} \over 2} \)
- Hàm số đồng biến trên khoảng \(({-1\over2};+\infty)\), nghịch biến trên khoảng \((-\infty; {-1\over2})\)
- Cực trị:
Hàm số đạt cực tiểu tại \(x={-1\over2}\); \(y_{CT}={-3\over 2}\)
- Giới hạn:
\(\mathop {\lim }\limits_{x \to \pm \infty } y = + \infty \)
Bảng biến thiên:
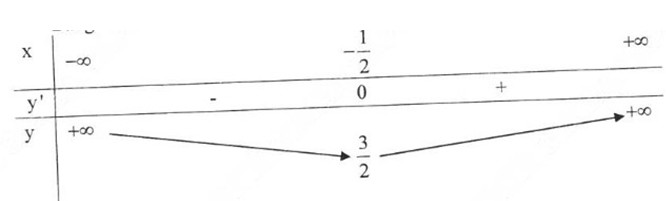
*Đồ thị
Đồ thị hàm số giao trục \(Ox\) tại hai điểm \((-1;0)\) và \((0;0)\)
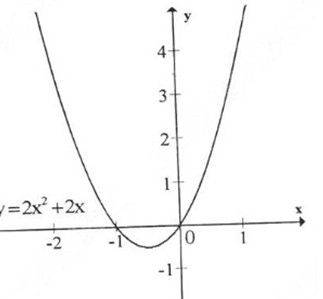
b) Tổng quát \(y = 2x^2+ 2mx + m -1\) có tập xác định \(D = \mathbb R\)
\(y' = 4x + 2m = 0 \Leftrightarrow x = {{ - m} \over 2}\)
Suy ra \(y’ >\) 0 với \(x > {{ - m} \over 2};y' < 0\) với \(x < {{ - m} \over 2}\) , tức là hàm số nghịch biến trên \(( - \infty ,{{ - m} \over 2})\) và đồng biến trên \(({{ - m} \over 2}, + \infty )\)
i) Để hàm số đồng biến trên khoảng \((-1, +∞)\) thì phải có điều kiện \(( - 1,{\rm{ }} + \infty ) \in ({{ - m} \over 2}, + \infty )\)
\( \Leftrightarrow {{ - m} \over 2} \le - 1 \Leftrightarrow m \ge 2\)
ii) Hàm số đạt cực trị tại \(x = {{ - m} \over 2}\) .
Để hàm số đạt cực trị trong khoảng \((-1, +∞)\), ta phải có:
\(\eqalign{
& {{ - m} \over 2} \in ( - 1, + \infty ) \cr
& \Leftrightarrow {{ - m} \over 2} > - 1 \Leftrightarrow 1 > {m \over 2} \Leftrightarrow m < 2 \cr} \)
c) (Cm) luôn cắt \(Ox\) tại hai điểm phân biệt \(x = {{ - m} \over 2}\)
\(⇔\) phương trình \(2x^2+ 2mx + m – 1 = 0\) có hai nghiệm phân biệt.
Ta có:
\(Δ’ = m^2– 2m + 2 = (m-1)^2+ 1 > 0 ∀m\)
Vậy (Cm) luôn cắt \(O x\) tại hai điểm phân biệt.
Bài 6 trang 45 SGK Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số \((C)\) của hàm số
\(f(x) = - {x^3} + 3{x^2} + 9x + 2\)
b) Giải bất phương trình \(f’(x-1)>0\)
c) Vẽ phương trình tiếp tuyến của đồ thị \((C)\)tại điểm có hoành độ \(x_0\), biết rằng \(f’’(x_0) = -6\)
Giải
a) Tập xác định: \(D =\mathbb R\)
* Sự biến thiên:
\(y' = - 3{x^2} + 6x + 9 = 0 \Leftrightarrow x = - 1,x = 3 \)
- Hàm số đồng biến trên khoảng: \((-1;3)\), nghịch biến trên khoảng \((-\infty; -1)\) và \((3;+\infty)\)
- Cực trị:
Hàm số đạt cực đại tại \(x=3\); \(y_{CĐ}=29\)
Hàm số đạt cực tiểu tại \(x=-1\); \(y_{CT}=-3\)
- Giới hạn:
\(\mathop {\lim }\limits_{x \to - \infty } f(x) = + \infty\)
\(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \)
-Bảng biến thiên:
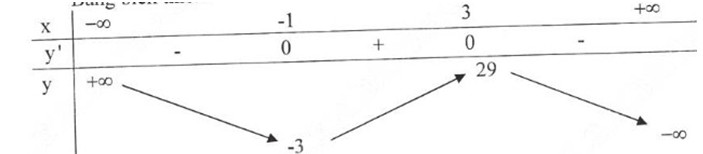
* Đồ thị
Đồ thị hàm số giao trục \(Oy\) tại điểm \((0;2)\)
Đồ thị hàm số nhận \(I(1;13)\) làm tâm đối xứng.
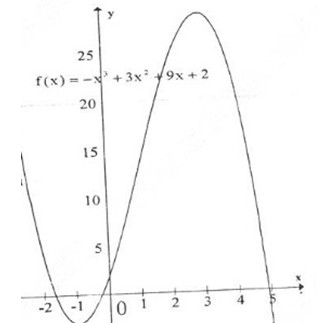
b) \(y=f(x) = f(x) = - {x^3} + 3{x^2} + 9x + 2\)
\(f’(x) = - 3{x^2} + 6x + 9 = 0\). Do đó:
\(f’(x-1)=-3(x-1)^2+6(x-1)+9\)
= \(-3x^2+ 12x = -3x(x-4) > 0 ⇔ 0 < x < 4\)
c) \(f’’(x) = -6x+6\)
\(f’’(x_0)= -6 ⇔ -6x_0+ 6 = -6 ⇔ x_0= 2\)
Do đó: \(f’(2) = 9, f(2) = 24\). Phương trình tiếp tuyến của \((C)\) tại \(x_0= 2\) là:
\(y=f’(2)(x-2) + f(2)\) hay \(y = 9x+6\).
Bài 7 trang 46 SGK Giải tích 12
a) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số:
\(y = x^3+ 3x^2+ 1\)
b) Dựa vào đồ thị \((C)\), biện luận số nghiệm của phương trình sau theo m
\({x^3} + 3{x^2} + 1 = {m \over 2}\)
c) Viết phương trình đường thẳng đi qua điểm cực đại và điểm cực tiểu của đồ thị \((C)\)
Giải
a) \(y = x^3+ 3x^2+ 1\)
Tập xác định: \(D =\mathbb R\)
* Sự biến thiên:
\(y’= 3x^2+ 6x = 3x(x+ 2)\)
\(y’=0 ⇔ x = 0, x = -2\).
- Hàm số đồng biến trên khoảng \((-\infty;-2)\) và \((0;+\infty)\), nghịch biến trên khoảng \((-2;0)\)
- Cực trị:
Hàm số đạt cực đại tại \(x=-2\); \(y_{CĐ}=5\)
Hàm số đạt cực tiểu tại \(x=0\); \(y_{CT}=1\).
- Giới hạn:
\(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty \cr} \)
- Bảng biến thiên:
Đồ thị:
Đồ thị hàm số giao \(Oy\) tại \((0;1)\)
Đồ thị hàm số nhận \(I(-1;3)\) làm tâm đối xứng.
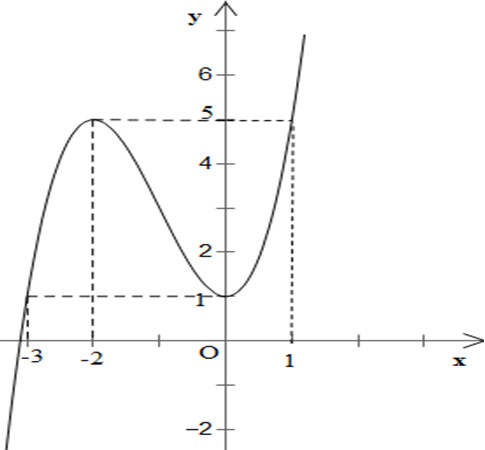
b) Số nghiệm của phương trình \({x^3} + 3{x^2} + 1 = {m \over 2}\) chính là số giao điểm của \((C)\) và đường thẳng \((d)\): \(y = {m \over 2}\)
Từ đồ thị ta thấy:
- Với \({m \over 2} < 1 \Leftrightarrow m < 2\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
- Với \({m \over 2} = 1 ⇔ m = 2\): (d) tiếp xúc với (C) tại 1 điểm và cắt (C) tạo 1 điểm, phương trình có hai nghiệm
- Với \(1 < {m \over 2} < 5 ⇔ 2<m<10\), phương trình có 3 nghiệm.
- Với \({m \over 2} = 5 \Leftrightarrow m = 10\): (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, phương trình có hai nghiệm.
- Với \({m \over 2} > 5 \Leftrightarrow m > 10\) : (d) cắt (C) tại 1 điểm, phương trình có 1 nghiệm
c) Điểm cực đại \((-2, 5)\), điểm cực tiểu \((0, 1)\).
Đường thẳng đi qua hai điểm này có phương trình là: \({{y - 1} \over 4} = {x \over { - 2}} \Leftrightarrow y = - 2x + 1\)
Bài 8 trang 46 SGK Giải tích 12
Cho hàm số:
\(f(x)= x^3– 3mx^2+ 3(2m-1)x + 1\) ( \(m\) là tham số)
a) Xác định \(m\) để hàm số đồng biến trên một tập xác định
b) Với giá trị nào của tham số \(m\), hàm số có một cực đại và một cực tiểu
c) Xác định \(m\) để \(f’’(x)>6x\)
Giải
a) \(y=f(x)= x^3– 3mx^2+ 3(2m-1)x + 1\)
Tập xác định: \(D =\mathbb R\)
\(y’= 3x^2-6mx + 3(2m-1) = 3(x^2– 2mx + 2m – 1)\)
Hàm số đồng biến trên \(D =\mathbb R ⇔ y’ ≥ 0, ∀x ∈ R\)
\(⇔ x^2– 2mx + 2m - 1≥0, ∀x ∈\mathbb R\)
\(⇔ Δ’ = m^2– 2m + 1 = (m-1)^2\le 0 ⇔ m =1\)
b) Hàm số có một cực đại và một cực tiểu
\(⇔\) phương trình \(y’= 0\) có hai nghiệm phân biệt
\(⇔ (m-1)^2> 0 ⇔ m≠1\)
c) \(f’’(x) = 6x – 6m > 6x\)
\(⇔ -6m > 0 ⇔ m < 0\)