Bài 1 trang 12 sgk hình học 12
Chứng minh rằng một đa diện có các mặt là những tam giác thì tổng số các mặt của nó là một số chẵn. Cho ví dụ
Giải:
Giả sử đa diện \((H)\) có \(m\) mặt. Vì mỗi mặt của \((H)\) có 3 cạnh, nên \(m\) mặt có \(3m\) cạnh. Nhưng mỗi cạnh của \((H)\) là cạnh chung của đúng hai mặt nên số cạnh của \((H)\) bằng \(c =\) \({{3m} \over 2}\). Do \(c\) là số nguyên dương nên \(m\) phải là số chẵn. Ví dụ : Số cạnh của tứ diện bằng sáu.
Bài 2 trang 12 sgk hình học 12
Chứng minh rằng một đa diện mà mỗi đỉnh của nó đều là đỉnh chung của số lẻ mặt thì tổng số các đỉnh của nó là một số chẵn. Cho ví dụ.
Giải :
Giả sử đa diện \((H)\) có các đỉnh là \(A_1, … A_d\) gọi \(m_1, … m_d\) lần lượt là số các mặt của \((H)\) nhận chúng là đỉnh chung. Như vậy mỗi đỉnh \(A_k\) có \(mk\) cạnh đi qua. Do mỗi cạnh của \((H)\) là cạnh chung của đúng hai mặt nên tổng số các cạnh của \(H\) bằng
\(c = {1 \over 2}({m_1} + {m_2} + ... + {m_d})\)
Vì \(c\) là số nguyên, \(m_1, … m_d\) là những số lẻ nên \(d\) phải là số chẵn. Ví dụ : Số đỉnh của hình chóp ngũ giác bằng sáu.
Bài 3 trang 12 sgk hình học 12
Chia một khối lập phương thành năm khối tứ diện.
Giải :
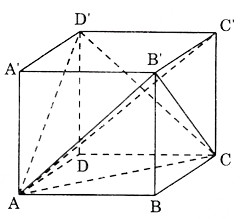
Chia khối lập phương \(ABCD.A'B'C'D'\) thành năm khối tứ diện như sau: \(A'B'CD', A'AB'D', BACB', C'B'CD', DACD'\).
Bài 4 trang 12 sách sgk hình học 12
Chia một khối lập phương thành sáu khối tứ diện bằng nhau.
Giải:
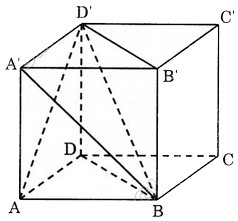
Chia lăng trụ \(ABD.A'B'D'\) thành ba tứ diện \(DABD', A'ABD', A'B'BD'\). Phép đối xứng qua \((ABD')\) biến \(DABD'\) thành \(A'ABD'\), phép đối xứng qua \((BA'D')\) biến \(A'ABD'\) thành \(A'B'BD'\) nên ba tứ diện \(DABD', A'ABD', A'B'BD'\) bằng nhau.
Làm tương tự đối với lăng trụ \(BCD.B'C'D'\) ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.