Toán học Giải bài 1, 2, 3 trang 77 SGK Giải tích

Bài 1 trang 77 sgk giải tích 12

Vẽ đồ thị của các hàm số:

a) y=4xy=4x;

b) y=(14)xy=(14)x.

Giải

a) Đồ thị hàm số y=4xy=4x 

Tập xác định: RR

Sự biến thiên:

y′=4xln4>0,∀x∈Ry′=4xln⁡4>0,∀x∈R

- Hàm số đồng biến trên RR

- Giới hạn đặc biệt:

   limx→−∞y=0limx→+∞y=+∞limx→−∞⁡y=0limx→+∞⁡y=+∞

Tiệm cận ngang: y=0y=0

- Bảng biến thiên:

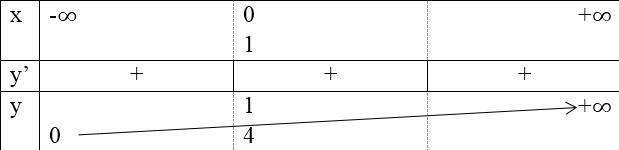
Đồ thị:

Đồ thị nằm hoàn toàn phía trên trục hoành, cắt trục tung tại các điểm (0;1)(0;1), đi qua điểm (1;4)(1;4) và qua các điểm (1/2;2)(1/2;2), (−1/2;1/2)(−1/2;1/2), (−1;1/4)(−1;1/4).

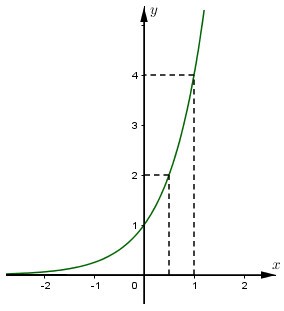
b) Đồ thị hàm số y=(14)xy=(14)x 

Tập xác định: RR

Sự biến thiên:

y′=−(14)xln4<0,∀x∈Ry′=−(14)xln⁡4<0,∀x∈R

- Hàm số nghịch biến trên RR

- Giới hạn:

  limx→−∞y=+∞limx→+∞y=0limx→−∞⁡y=+∞limx→+∞⁡y=0

Tiệm cận ngang y=0y=0

- Bảng biến thiên:

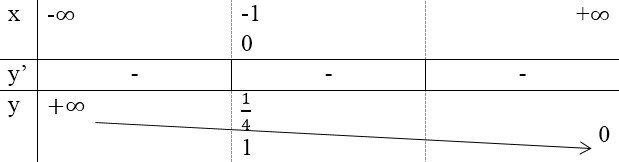
Đồ thị:

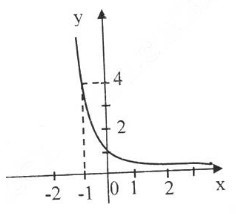
Đồ thị hàm số nằm hoàn toàn về phía trên trục hoành, cắt trục tung tại điểm (0; 1), đi qua điểm (1; 1414) và qua các điểm (−12−12; 2), (-1;4). 

Bài 2 trang 77 sgk giải tích 12

Tính đạo hàm của các hàm số:

a) y=2xex+3sin2xy=2xex+3sin2x;

b) y=5x2−2xcosxy=5x2−2xcosx;

c) y=x+13xy=x+13x.

Giải:

a) y′=(2xex)′+3(sin2x)′=2.ex+2x(ex)′y′=(2xex)′+3(sin⁡2x)′=2.ex+2x(ex)′

+3.2cos2x+3.2cos2x=2(1+x)ex+6cos2x2(1+x)ex+6cos2x

b) y′=10x−(2xcosx)′y′=10x−(2xcosx)′=10x−(2xln2.cosx−2x.sinx)=10x−(2xln2.cosx−2x.sinx)=10x−2x(ln2.cosx−sinx)=10x−2x(ln2.cosx−sinx).

c) 

y′=(x+1)′.3−x+(x+1)(3−x)′=3−x+(x+1)3−xln3,(−x)′=3−x[1−ln3(x+1)]=1−(x+1)ln33xy′=(x+1)′.3−x+(x+1)(3−x)′=3−x+(x+1)3−xln⁡3,(−x)′=3−x[1−ln⁡3(x+1)]=1−(x+1)ln⁡33x

Bài 3 trang 77 sgk giải tích 12

Tìm tập xác định của các hàm số:

a) y=log2(5−2x)y=log2(5−2x) ;

b) y=log3(x2−2x)y=log3(x2−2x) ;

c) y=log15(x2−4x+3)y=log15(x2−4x+3);

d) y=log0,43x+11−xy=log0,43x+11−x.

Giải:

Hàm số y=logaφ(x)y=logaφ(x) ( cơ số a dương, khác 1 đã cho) xác định khi và chỉ khi φ(x)φ(x) > 0. Vì vậy hàm số y=logaφ(x)y=logaφ(x) có tập xác định là tập nghiệm bất phương trình φ(x)φ(x) > 0.

a) ta có 5−2x>05−2x>0 ⇔x<52⇔x<52. Vậy hàm số y=log2(5−2x)y=log2(5−2x) có tập xác định là khoảng (−∞;52)(−∞;52).

b) Ta có x2−2x>0⇔x<0x2−2x>0⇔x<0 hoặc x>2x>2 . Vậy hàm số y=log3(x2−2x)y=log3(x2−2x) có tập xác định là khoảng (−∞;0)∪(2;+∞)(−∞;0)∪(2;+∞).

c) Ta có x2−4x+3>0⇔x<1x2−4x+3>0⇔x<1 hoặc x>3x>3. vậy hàm số y=log15(x2−4x+3)y=log15(x2−4x+3) có tập xác định là (−∞;1)∪(3;+∞)(−∞;1)∪(3;+∞).

d) Ta có 3x+21−x>03x+21−x>0 ⇔(3x+2)(1−x)>0⇔(3x+2)(1−x)>0 ⇔⇔ −23<x<1−23<x<1.

Vậy hàm số y=log0,43x+11−xy=log0,43x+11−x có tập xác định là khoảng (−23;1)(−23;1).