Bài 1 trang 143 SGK Giải tích 12
Thế nào là phần thực, phần ảo, modun của số phức?
Viết công thức tính môdun của một số phức theo phần thực và phần ảo của nó.
Giải
- Mỗi biểu thức dạng \(a+bi\), trong đó \(a, b ∈ R, i^2= -1\) được gọi làm một số phức.
- Với số phức \(z = a + bi\), ta gọi \(a\) là phần thực, số \(b\) gọi là phần ảo của \(z\).
- Ta có \(z = a + bi\) thì môdun của \(z\) là \(|z| = |a + bi| = \sqrt {{a^2} + {b^2}} \).
Bài 2 trang 143 SGK Giải tích 12
Tìm mối liên hệ giữa khái niệm môdun và khái niệm giá trị tuyệt đối của một số thực.
Giải
- Nếu số thực \(x\) là một số thực thì môdun \(x\) chính là giá trị tuyệt đối của số phức \(z\).
- Nếu số phức \(z\) không phải là một số thực thì chỉ có môdun của \(z\), không có khái niệm giá trị tuyệt đối của \(z\).
Bài 3 trang 143 SGK Giải tích 12
Nêu định nghĩa số phức liên hợp của số phức \(z\). Số phức nào bằng số phức liên hợp của nó?
Giải
*Cho số phức \(z = a + bi\).
Ta gọi số phức \(a – bi\) là số phức liên hợp của \(z\) và kí hiệu là \(\bar z\).
Vậy ta có \(z = a + bi\) thì \(\bar z= a – bi\)
*Số phức \(z\) bằng số phức liên hợp của nó \(⇔ a = a\) và \(b = -b\)
\(⇔ a ∈ R\) và \(b = 0 ⇔ z\) là một số thực.
Bài 4 trang 143 SGK Giải tích 12
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo trong các hình a), b), c) sau:
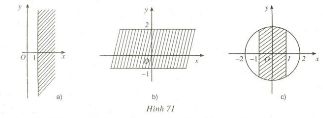
Giải
Giả sử \(z = x + yi\) (\(x,y \in \mathbb R\)), khi đó số phức \(z\) được biểu diễn bởi điểm \(M(x, y)\) trên mặt phẳng tọa độ \(Oxy\).
a) Trên hình 71.a (SGK), điểm biểu diễn ở phần gạch chéo có hoành độ có hoành độ \(x ≥ 1\), tung độ \(y\) tùy ý.
Vậy số phức có phần thực lớn hơn hoặc bằng \(-1\) có điểm biểu diễn ở hình 71.a (SGK)
b) Trên hình 71.b(SGK), điểm biểu diễn có tung độ \(y ∈ [1, 2]\), hoành độ \(x\) tùy ý.
Vậy số phức có phần ảo thuộc đoạn \([-1, 2]\)
c) Trên hình 71.c (SGK), hình biểu diễn \(z\) có hoành độ \(x ∈ [-1, 1]\) và \(x^2+y^2≤ 4\) (vì \(|z| ≤ 4\)).
Vậy số phức có phần thực thuộc đoạn \([-1, 1]\) và môdun không vượt quá \(2\).