Bài 5 trang 26 SGK Hình học 12
Cho hình chóp tam giác \(O.ABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc với nhau và \(OA = a, OB = b, OC = c\). Hãy tính đường cao \(OH\) của hình chóp.
Giải
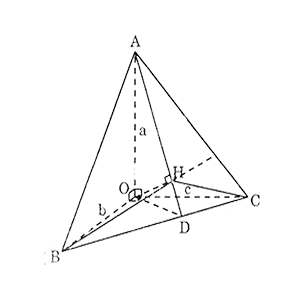
Kẻ \(AD\bot BC, OH \bot AD\) thì dễ thấy \(OH\) chính là đường cao của hình chóp.
Vì \(OD.BC = OB.OC\) nên \(OD ={{bc} \over {\sqrt {{b^2} + {c^2}} }}\) . Từ đó suy ra
\(AD = \sqrt {{a^2} + {{{b^2}{c^2}} \over {{b^2} + {c^2}}}}\) = \(\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}\) .
Vì \(OH.AD = OA.OD\) nên
\(OH = {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}} = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Bài 6 trang 26 SGK Hình học 12
Cho hình chóp tam giác \(S.ABC\) có cạnh \(AB\) bằng \(a\). Các cạnh bên \(SA, SB, SC\) tạo với đáy một góc \(60^0\). Gọi \(D\) là giao điểm của \(SA\) với mặt phẳng qua \(BC\) và vuông góc với \(SA\).
a) Tính tỉ số thể tích của hai khối chóp \(S.DBC\) và \(S.ABC\).
b) Tính thể tích của khối chóp \(S.DBC\).
Giải
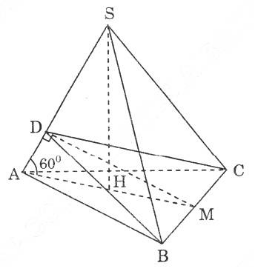
a) Vì hình chóp \(S.ABC\) là hình chóp đều nên chân đường cao \(H\) là tâm của đường tròn ngoại tiếp đáy, theo giả thiết, ta có: góc \(SAH = 60^0\). Gọi \(M\) là trung điểm của cạnh \(BC\) thì \(AM\) là đường cao của tam giác đều \(ABC\):
\(AM = {{a\sqrt 3 } \over 2}\)
\(AH = {2 \over 3}.AM = {{a\sqrt 3 } \over 3}\)
Từ đây, ta có:\(SA = {{AH} \over {c{\rm{os}}{{60}^0}}}\) = \({{2a\sqrt 3 } \over 3}\)
\(AD = AM.cos 60^0\) = \({{a\sqrt 3 } \over 4}\)
\(\Rightarrow SD = SA - AD = {{5a\sqrt 3 } \over {12}}\)
Áp dụng công thức tỉ số thể tích trong bài tập 4, 3 (trang 37 SGK) ta được:
\({{{V_{S.DBC}}} \over {{V_{S.ABC}}}} = {{SD} \over {SA}}.{{SB} \over {SB}}.{{SC} \over {SC}} = {{5a\sqrt 3 } \over {12}}:{{2a\sqrt 3 } \over 3} = {5 \over 8}\)
b) Ta có: \(S_{ABC}\) = \({{{a^2}\sqrt 3 } \over 4}\); \(SH = AH.tan60^0 = a\)
\( \Rightarrow {V_{S.ABC}} = {1 \over 3}.SH.{S_{ABC}}\) \( \Rightarrow {V_{S.ABC}} = {{{a^3}\sqrt 3 } \over {12}}\)
Từ kết quả câu a) ta có:
\({V_{S.DBC}} = {5 \over 8}.{V_{S.ABC}}\) \( \Rightarrow {V_{S.BDC}} = {5 \over 8}.{{{a^3}\sqrt 3 } \over {12}}\)
\( \Rightarrow {V_{S.DBC}} = {{5{a^3}\sqrt 3 } \over {96}}\)
Bài 7 trang 26 SGK Hình học 12
Cho hình chóp tam giác \(S.ABC\) có \(AB = 5a, BC = 6a, CA = 7a\). Các mặt bên \(SAB, SBC, SCA\) tạo với đáy một góc \(60^0\). Tính thể tích của khối chóp đó.
Giải
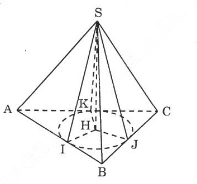
Kẻ \(SH \bot (ABC)\) và từ \(H\) kẻ \(HI \bot AB, HJ \bot BC, HK \bot CA\).
Từ định lý ba đường vuông góc, ta suy ra:
\(SI \bot AB, SJ \bot BC, SK \bot AC\) do đó:
\(\widehat {SIH} = \widehat {SJH} = \widehat {SKH} = {60^0}\)
Từ đây ta có: \(△SIH = △SJH = △SKH\)
\( \Rightarrow IH = JH = KH\)
\( \Rightarrow H\) là tâm đường tròn nội tiếp \(△ABC\).
Tam giác \(ABC\) có chu vi:
\(2p = AB + BC + CA = 18a\)
\( \Rightarrow p = 9a\)
Ta có: \(p - AB = 4a\)
\( p - BC = 3a\)
\( p - CA = 2a\)
Theo công thức Hê-rông, ta có: \(S = \sqrt {9a.4a.3a.2a} = 6{a^2}\sqrt 6 \)
Bán kính của đường tròn nội tiếp tam giác \(ABC\):
\(IH = r = {{{S_{ABC}}} \over p} = {{6{a^2}\sqrt 6 } \over {9a}} \Rightarrow IH = {{2a\sqrt 6 } \over 3}\)
Đường cao \(SH\) của khối chóp:
\(SH = r . tan60^0\) = \({{2a\sqrt 6 } \over 3}.\sqrt 3 = 2a\sqrt 2 \)
Thể tích khối chóp:
\({V_{S.ABC}} = {1 \over 3}.2a\sqrt 2 .6{a^2}\sqrt 6 = 8{a^3}\sqrt 3 \)
Bài 8 trang 26 SGK Hình học 12
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(SA\) vuông góc với đáy và \(AB = a, AD = b, SA =c\). Lấy các điểm \(B', D'\) theo thứ tự thuộc \(SB, SD\) sao cho \(AB'\) vuông góc với \(SB, AD'\) vuông góc với \(SD\). Mặt phẳng \((AB'D')\) cắt \(SC\) tại \(C'\). Tính thể tích khối chóp \(S.AB'C'D'\).
Giải
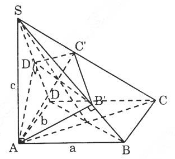
Ta có \(BC \bot (SAB)\Rightarrow BC\bot AB'\)
Theo giả thiết \(SB \bot AB'\)
\(AB' \bot (SBC) \Rightarrow AB' \bot SC\) (1)
Chứng minh tương tự ta có:
\(AD' \bot SC\) (2)
Từ (1) và (2) suy ra \(SC \bot (AB'C'D')\) hay \(SC\) là đường cao của hình chóp \(S.AB'C'D'\).
Từ \(AB' \bot (SBC)\) \( \Rightarrow AB' \bot B'C'\)
Tương tự ta có: \(AD' \bot D'C'\)
Từ các kết quả trên, ta được:
\({V_{AB'C'D'}} = {1 \over 3}.SC'.{1 \over 2}(AB'.B'C' + AD'.D'C')\)
= \({1 \over 6}SC'.(AB'.B'C' + AD'.D'C')\) (*)
Ta tính các yếu tố trên.
Tam giác vuông \(SAB\) có \(AB'\) là đường cao, nên ta có:
\({1 \over {AB{'^2}}} = {1 \over {{a^2}}} + {1 \over {{c^2}}} \Rightarrow AB{'^2} = {{{a^2}{c^2}} \over {{a^2} + {c^2}}}\)
\( \Rightarrow AB' = {{ac} \over {\sqrt {{a^2} + {c^2}} }}\)
Tương tự, ta có:
\(AD{'^2} = {{{b^2}{c^2}} \over {{b^2} + {c^2}}} \Rightarrow AD' = {{bc} \over {\sqrt {{b^2} + {c^2}} }}\)
Ta lại có: \(SC^2 = AC^2 + AS^2 = a^2 + b^2 + c^2\)
\( \Rightarrow SC = \sqrt {{a^2} + {b^2} + {c^2}} \)
Trong tam giác vuông \(SAC, AC'\) là đường cao thuộc cạnh huyền
\(SC'.SC = SA^2\) \( \Rightarrow SC' = {{S{A^2}} \over {SC}} = {{{c^2}} \over {\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\(∆SBC\) đồng dạng \(∆SC'B'\) \( \Rightarrow {{B'C'} \over {BC}} = {{SC'} \over {SB}}\)
\( \Rightarrow B'C' = {{SC'.BC} \over {SB}} = {{b{c^2}} \over {\sqrt {{a^2} + {c^2}} \sqrt {{a^2} + {b^2} + {c^2}} }}\)
Tương tự ta có: \(D'C' = {{{c^2}a} \over {\sqrt {{b^2} + {c^2}} \sqrt {{a^2} + {b^2} + {c^2}} }}\)
Thay các kết quả này vào (*) ta được:
\(V = {1 \over 6}.{{ab{c^5}({a^2} + {b^2} + 2{c^2})} \over {({a^2} + {c^2})({b^2} + {c^2})({a^2} + {b^2} + {c^2})}}\)