Lớp 11 - SBT Toán học Giải bài 3.8, 3.9, 3.10, 3.11 trang 140 Sách bài tập Hình học 11
Bài 3.8 trang 140 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Gọi G là trọng tâm của tam giác ABC. Chứng minh rằng:
\(\overrightarrow {G{\rm{D}}} .\overrightarrow {GA} + \overrightarrow {G{\rm{D}}} .\overrightarrow {GB} + \overrightarrow {G{\rm{D}}} .\overrightarrow {GC} = 0\)
Giải:
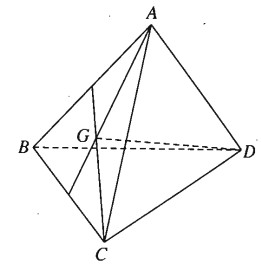
Ta có:
\(\eqalign{
& \overrightarrow {G{\rm{D}}} .\overrightarrow {GA} + \overrightarrow {GD} .\overrightarrow {GB} + \overrightarrow {GD} .\overrightarrow {GC} \cr
& = \overrightarrow {GD} .\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) \cr
& = \overrightarrow {GD} .\overrightarrow 0 = 0 \cr} \)
(Vì G là trọng tâm của tam giác ABCD nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \) )
Bài 3.9 trang 140 Sách bài tập (SBT) Hình học 11
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn AC, BD, AD và có MN = PQ . Chứng minh rằng AB ⊥ CD.
Giải:
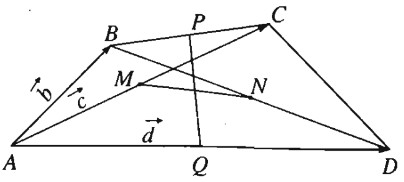
Ta cần chứng minh \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0\)
Đặt \(\overrightarrow {AB} = \overrightarrow b ,\,\,\overrightarrow {AC} = \overrightarrow c ,\,\,\overrightarrow {AD} = \overrightarrow d \). Ta có:
\(\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = - {1 \over 2}\overrightarrow {AC} + {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\)
Suy ra \(\overrightarrow {MN} = {1 \over 2}\left( {\overrightarrow b + \overrightarrow d - \overrightarrow c } \right)\)
\(\eqalign{
& \overrightarrow {QP} = \overrightarrow {QA} + \overrightarrow {AP} \cr
& = - {1 \over 2}\overrightarrow {A{\rm{D}}} + {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \cr
& = {1 \over 2}\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right) \cr} \)
Theo giả thiết ta có:
\(MN = PQ \Leftrightarrow {\overrightarrow {MN} ^2} = {\overrightarrow {QP} ^2}\)
\(\eqalign{
& {\left( {\overrightarrow b + \overrightarrow d - \overrightarrow c } \right)^2} = {\left( {\overrightarrow b + \overrightarrow c - \overrightarrow d } \right)^2} \cr
& \Leftrightarrow \overrightarrow b .\overrightarrow d - \overrightarrow b .\overrightarrow c = \overrightarrow b .\overrightarrow c - \overrightarrow b .\overrightarrow d \cr
& \Leftrightarrow 2\overrightarrow b .\overrightarrow d - 2\overrightarrow b .\overrightarrow c = 0 \cr
& \Leftrightarrow \overrightarrow b .\left( {\overrightarrow d - \overrightarrow c } \right) = 0 \cr
& \Leftrightarrow \overrightarrow {AB} .\left( {\overrightarrow {A{\rm{D}}} - \overrightarrow {AC} } \right) = 0 \cr
& \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0 \Leftrightarrow \overrightarrow {AB} \bot \overrightarrow {C{\rm{D}}} \cr} \)
Bài 3.10 trang 140 Sách bài tập (SBT) Hình học 11
Cho hình chóp tam giác S.ABC có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} \).
Giải:
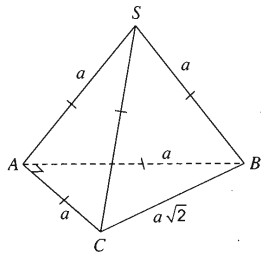
Ta tính côsin của góc giữa hai vectơ \(\overrightarrow {SC} \) và \(\overrightarrow {AB} \). Ta có
\(\eqalign{
& \cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{\overrightarrow {SC} .\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr
& = {{\left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} } \over {{a^2}}} = {{\overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} } \over {{a^2}}} \cr} \)
Theo giả thiết ta suy ra hình chóp có các tam giác đều là SAB, SAC và các tam giác vuông là ABC vuông tại A và SBC vuông tại S.
Do đó \(\overrightarrow {SA} .\overrightarrow {AB} = a.a.\cos 120^\circ = - {{{a^2}} \over 2}\) và \(\overrightarrow {AC} .\overrightarrow {AB} = 0\)
Vậy \(\cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{ - {{{a^2}} \over 2} + 0} \over {{a^2}}} = - {1 \over 2}\)
Hay \(\left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {120^0}\)
Vậy góc giữa hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {SC} ) bằng 120°
Bài 3.11 trang 141 Sách bài tập (SBT) Hình học 11
Cho hình chóp A.ABC có \(SA = SB = SC = AB = AC = a\) và \(BC = a\sqrt 2 \). Tính góc giữa hai đường thẳng AB và SC.
Giải:
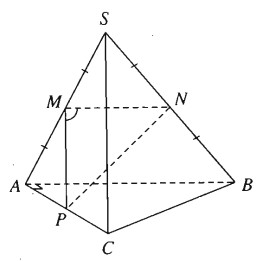
Cách thứ nhất
Dễ thấy tam giác ABC vuông tại A nên \(\overrightarrow {AC} .\overrightarrow {AB} = 0\) và tam giác SAB đều nên \(\left( {\overrightarrow {SA} ,\overrightarrow {AB} } \right) = {120^0}\).
\(\eqalign{
& \overrightarrow {SC} .\overrightarrow {AB} = \left( {\overrightarrow {SA} + \overrightarrow {AC} } \right).\overrightarrow {AB} \cr
& = \overrightarrow {SA} .\overrightarrow {AB} + \overrightarrow {AC} .\overrightarrow {AB} \cr
& \left| {\overrightarrow {SA} } \right|.\left| {\overrightarrow {AB} } \right|.\cos 120^\circ = - {{{a^2}} \over 2} \cr
& \Rightarrow \cos \left( {\overrightarrow {SC} ,\overrightarrow {AB} } \right) = {{\overrightarrow {SC} .\overrightarrow {AB} } \over {\left| {\overrightarrow {SC} } \right|.\left| {\overrightarrow {AB} } \right|}} \cr
& = {{ - {{{a^2}} \over 2}} \over {{a^2}}} = - {1 \over 2} \cr}\)
Do đó góc giữa hai đường thẳng SC và AB bằng 60°
Cách thứ hai
Gọi M, N, P lần lượt là trung điểm của SA, SB. AC. Để tính góc giữa hai đường thẳng SC và AB, ta cần tính \(\widehat {NMP}\).
Ta có
\(NB = MP = {a \over 2},S{P^2} = {{3{a^2}} \over 4},B{P^2} = {{5{a^2}} \over 4}\)
\(P{B^2} + S{P^2} = 2N{P^2} + {{S{B^2}} \over 2} \Rightarrow N{P^2} = {{3{{\rm{a}}^2}} \over 4}\)
Mặt khác:
\(N{P^2} = N{M^2} + M{P^2} - 2MN.MP\cos \widehat {NMP}\)
\( \Rightarrow \cos \widehat {NMP} = - {{{{{a^2}} \over 4}} \over {2.{a \over 2}.{a \over 2}}} = - {1 \over 2} \Rightarrow \widehat {NMP} = {120^0}\)
Vậy góc giữa hai đường thẳng SC và AB bằng 60°.
congdong.edu.vn