Lớp 11 - SBT Toán học Giải bài 3.44, 3.45, 3.46 trang 164 Sách bài tập Hình học 11
Bài 3.44 trang 164 Sách bài tập (SBT) Hình học 11
Hình chóp tam giác S.ABC có đáy là tam giác đều ABC cạnh 7a, có cạnh SC vuông góc với mặt phẳng đáy (ABC) và SC = 7a.
a) Tính góc giữa SA và BC.
b) Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC.
Giải:
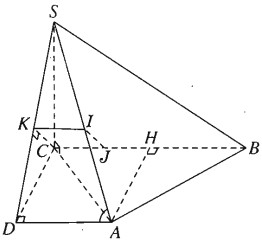
a) Gọi H là trung điểm của đoạn BC. Qua A vẽ AD song song với BC và bằng đoạn HC thì góc giữa BC và SA là góc \(\widehat {SA{\rm{D}}}\). Theo định lí ba đường vuông góc, ta có SD⊥DA và khi đó:
\(\cos \widehat {SAD} = {{AD} \over {SA}} = {{HC} \over {SA}} = {{{{7a} \over 2}} \over {7a\sqrt 2 }} = {{\sqrt 2 } \over 4}\)
Vậy góc giữa BC và SA được xác định sao cho \(\cos \widehat {SAD} = {{\sqrt 2 } \over 4}\)
Vì \(BC\parallel A{\rm{D}}\) nên BC song song với mặt phẳng (SAD). Do đó khoảng cách giữa SA và BC chính là khoảng cách từ đường thẳng BC đến mặt phẳng (SAD).
Ta kẻ CK⊥SD, suy ra CK⊥(SAD), do đó CK chính là khoảng cách nói trên. Xét tam giác vuông SCD với đường cao CK xuất phát từ đỉnh góc vuông C ta có hệ thức:
\({1 \over {C{K^2}}} = {1 \over {S{C^2}}} + {1 \over {C{D^2}}} \Rightarrow {1 \over {C{K^2}}} = {1 \over {{{\left( {7{\rm{a}}} \right)}^2}}} + {1 \over {{{\left( {{{7{\rm{a}}\sqrt 3 } \over 2}} \right)}^2}}}\)
(vì \(CD = AH = {{BC\sqrt 3 } \over 2} = {{7{\rm{a}}\sqrt 3 } \over 2}\))
Do đó \({1 \over {C{K^2}}} = {1 \over {49{{\rm{a}}^2}}} + {4 \over {3.49{{\rm{a}}^2}}} = {{3 + 4} \over {3.49{{\rm{a}}^2}}} = {1 \over {21{{\rm{a}}^2}}}\)
Vậy \(CK = a\sqrt {21} \)
Chú ý. Nếu kẻ \(KI\parallel A{\rm{D}}\) và kẻ \(IJ\parallel CK\) thì IJ là đoạn vuông góc chung của SA và BC.
Bài 3.45 trang 164 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi
\(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\)
Giải:
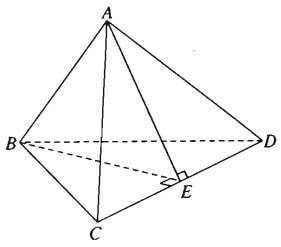
Giả sử AB⊥CD ta phải chứng minh \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\).
Thật vậy, kẻ BE⊥CD tại E, do AB⊥CD ta suy ra CD⊥(ABE) nên CD⊥AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
\(\eqalign{
& A{C^2} = A{{\rm{E}}^2} + C{E^2} \cr
& B{{\rm{D}}^2} = B{E^2} + E{{\rm{D}}^2} \cr
& B{C^2} = A{{\rm{E}}^2} + E{C^2} \cr
& {\rm{A}}{{\rm{D}}^2} = A{E^2} + E{{\rm{D}}^2} \cr} \)
Từ đó ta suy ra \(A{C^2} + B{{\rm{D}}^2} = A{D^2} + B{C^2}\)
Ngược lại nếu tứ diện ABCD có \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\) thì: \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2}\).
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = {k^2}\) thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho \(I{H^2} = {{{k^2}} \over {2C{\rm{D}}}}\).
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD⊥AB.
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = - {k^2}\) thì ta có và đưa về trường hợp xét như trên \(A{D^2} - A{C^2} = B{{\rm{D}}^2} - B{C^2} = - {k^2}\).
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi \(A{B^2} + C{D^2} = A{C^2} + B{C^2}\).
Bài 3.46 trang 164 Sách bài tập (SBT) Hình học 11
Cho hình lập phương ABCD.A’B’C’D’. Hãy tính góc của các cặp đường thẳng sau đây:
a) AB’ và BC’
b) AC’ và CD’
Giải:
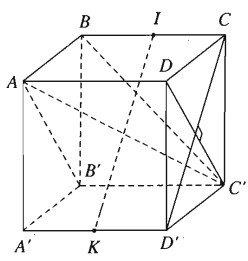
a) Ta có \(AB'\parallel DC'\). Gọi là góc giữa AB’và BC’, khi đó \(\alpha = \widehat {DC'B}\).
Vì tam giác BC’D đều nên \(\alpha = {60^0}\)
b) Gọi \(\beta \) là góc giữa AC’ và CD’.
Vì CD’⊥C’D và CD’⊥AD
( do AD⊥(CDD’C’)
Ta suy ra CD’⊥(ADC’B’)
Vậy CD’⊥AC’ hay \(\beta = {90^0}\)
Chú ý. Ta có thể chứng minh \(\beta = {90^0}\) bằng cách khác như sau:
Gọi I và K lần lượt là trung điểm của các cạnh BC và A’D’. Ta có \(IK\parallel C{\rm{D}}'\). Dễ dàng chứng minh được AIC’K là một hình bình hành có bốn cạnh bằng nhau và đó là một hình thoi. Vậy AC’⊥IK hay AC’⊥CD’ và góc \(\beta = {90^0}\).
congdong.edu.vn