Lớp 11 - SBT Toán học Giải bài 1.13, 1.14, 1.15, 1.16 trang 154, 155 Sách bài tập Đại số và giải tích 11
Bài 1.13 trang 154 Sách bài tập (SBT) Đại số và giải tích 11
Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng 3 và công bội \(q = {2 \over 3}\)
Giải:
ĐS: \({u_n} = {\left( {{2 \over 3}} \right)^{n - 1}}\)
Bài 1.14 trang 154 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số \(\left( {{b_n}} \right)\) có số hạng tổng quát là \({b_n} = \sin \alpha + {\sin ^2}\alpha + ... + {\sin ^n}\alpha \) với \(\alpha \ne {\pi \over 2} + k\pi \). Tìm giới hạn của \(\left( {{b_n}} \right)\)
Giải:
Dãy số: \(\sin \alpha ,...,{\sin ^n}\alpha ,...\) với \(\alpha \ne {\pi \over 2} + k\pi \), là một cấp số nhân vô hạn, công bội \(q = \sin \alpha \)
Vì \(\left| {\sin \alpha } \right| < 1\) với \(\alpha \ne {\pi \over 2} + k\pi \) nên \(\left( {{{\sin }^n}\alpha } \right)\) là một cấp số nhân lùi vô hạn.
Hơn nữa, \({b_n} = \sin \alpha + {\sin ^2}\alpha + ... + {\sin ^n}\alpha = {S_n}\)
Do đó, \(\lim {b_n} = \sin \alpha + {\sin ^2}\alpha + ... + {\sin ^n}\alpha + ... = {{\sin \alpha } \over {1 - \sin \alpha }}\)
Bài 1.15 trang 155 Sách bài tập (SBT) Đại số và giải tích 11
Cho số thập phân vô hạn tuần hoàn a = 34,121212... (chu kì là 12). Hãy viết a dưới dạng một phân số.
Giải:
Giải tương tự Ví dụ 13, ta có \(a = 34,121212... = {{1126} \over {33}}\)
Bài 1.16 trang 155 Sách bài tập (SBT) Đại số và giải tích 11
Giả sử ABC là tam giác vuông cân tại A với độ dài cạnh góc vuông bằng 1. Ta tạo ra các hình vuông theo các bước sau đây :
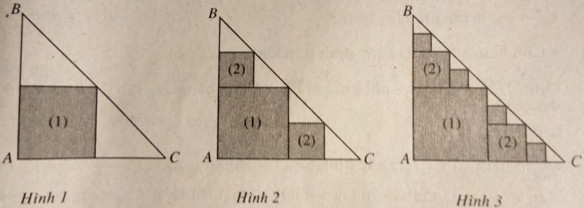
- Bước 1: Dựng hình vuông màu xám có mộtđỉnhA, ba đỉnh còn lại là các trung điểm của ba cạnhAB, BC và AC (H.1). Kí hiệu hình vuông này là (1).
- Bước2 : Với 2 tam giác vuông cân màu trắng còn lại như trong hình 1, ta lại tạo được 2 hình vuông màu xám khác theo cách trên, kí hiệu là (2) (H.2).
- Bước 3: Với 4 tam giác vuông cân màu trắng như trong hình 2, ta lại tạo được 4 hình vuông mới màu xámtheo cách trên (H.3).
- …
- Bước thứ n :Ở bước này ta có \({2^{n - 1}}\) hình vuông mới màu xám được tạo thành theo cách trên, kí hiệu là (n)
a) Gọi \({u_n}\) là tổng diện tích của tất cả các hình vuông mới được tạo thành ở bước thứ n. Chứng minh rằng \({u_n} = {1 \over {{2^{n + 1}}}}\)
b) Gọi \({S_n}\) là tổng diện tích của tất cả các hình vuông màu xám có được sau n bước. Quan sát hình vẽ để dự đoán giới hạn của \({S_n}\) khi \(n \to + \infty \). Chứng minh dự đoán đó.
Giải:
a) Chứng minh bằng quy nạp \({u_n} = {1 \over {{2^{n + 1}}}}\) (1)
- Với n = 1, một hình vuông được tạo thành có diện tích là \({u_1} = {1 \over {{2^2}}}\)
Vậy (1) đúng.
- Giả sử công thức (1) đúng với \(n = k\left( {k \ge 1} \right)\) nghĩa là \({u_k} = {1 \over {{2^{k + 1}}}}\). Ta cần chứng minh (1) đúng với \(n = k + 1\) tức là chứng minh \({u_{k + 1}} = {1 \over {{2^{k + 2}}}}\)
Thật vậy, ở bước thứ k ta có \({2^{k - 1}}\) hình vuông mới màu xám được tạo thành.Ứng với mỗi hình vuông này ta lại tạo được hai hình vuông mới trong bước thứ k + 1
Tổng diện tích của hai hình vuông mới nàytrong bước thứ k + 1 bằng nửa diện tích của hình vuông tương ứng bước thứ k
Do đó, tổng diện tích tất cả các hình vuông mới có được trong bước thứ k + 1 là \({u_{k + 1}} = {1 \over 2}.{1 \over {{2^{k + 1}}}} = {1 \over {{2^{k + 2}}}}\) Vậy (1) đúng với n = k + 1
- Kết luận: Với mọi n nguyên dương ta luôn có \({u_n} = {1 \over {{2^{n + 1}}}}\)
b) Dự đoán : \({S_n} \to {1 \over 2}{S_{ABC}}\) khi \(n \to + \infty \) hay \(\lim {S_n} = {1 \over 2}\)
Chứng minh :
\(\eqalign{
& {S_n} = {u_1} + {u_2} + ... + {u_n} \cr
& = {1 \over {{2^2}}} + {1 \over {{2^3}}} + ... + {1 \over {{2^{n + 1}}}} \cr
& = {1 \over 2} - {1 \over {{2^{n + 1}}}} \cr}\)
Từ đó suy ra \(\lim {S_n} = {1 \over 2}\)
congdong.edu.vn