Lớp 11 - SBT Toán học Giải bài 3.12, 3.13, 3.14, 3.15 trang 141 Sách bài tập Hình học 11
Bài 3.12 trang 141 Sách bài tập (SBT) Hình học 11
Chứng minh rằng một đường thẳng vuông góc với một trong hai đường thằng song song thì vuông góc với đường thẳng kia.
Giải:
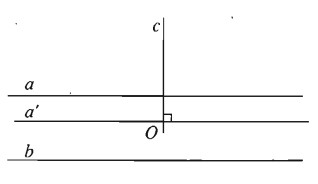
Giả sử \(a\parallel b\) và \(c \bot a\). Lấy điểm O bất kì trên c, kẻ \(a'\parallel a\) qua O suy ra \(\widehat {cOa'} = {90^0}\). Dễ thấy \(a'\parallel b\) nên \(\widehat {cOa'}\) chính là góc giữa hai đường thằng c và b, do đó \(c \bot b\).
Bài 3.13 trang 141 Sách bài tập (SBT) Hình học 11
Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau ( hình hộp như vậy còn được gọi là hình hộp thoi). Chứng minh rằng AC ⊥ B’D’
Giải:
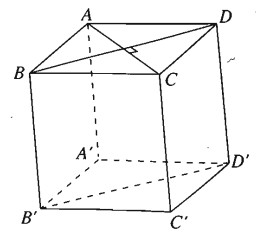
Từ giả thiết suy ra tứ giác ABCD là hình thoi, do đó AC ⊥ BD
Dễ thấy mặt chéo BDD’B’ của hình hộp đã cho là hình bình hành, do đó \(BD\parallel B'D'\). Từ đó, theo bài 3.12 suy ra AC ⊥ B’D’.
Bài 3.14 trang 141 Sách bài tập (SBT) Hình học 11
Cho hình hộp thoi ABCD.A’B’C’D’ có tất cả các cạnh bằng a và \(\widehat {ABC} = \widehat {B'BA} = \widehat {B'BC} = {60^0}\). Chứng minh tứ giác A’B’CD là hình vuông.
Giải:
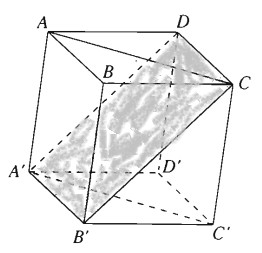
Trước hết dễ thấy tứ giác A’B’CD là hình bình hành, ngoài ra \(B'C = a = C{\rm{D}}\) nên nó là hình thoi. Ta chứng minh hình thoi A’B’CD là hình vuông. Ta có:
\(\eqalign{
& \overrightarrow {CB'} .\overrightarrow {CD} = \left( {\overrightarrow {CB} + \overrightarrow {BB'} } \right).\overrightarrow {BA} \cr
& = \overrightarrow {CB} .\overrightarrow {BA} + \overrightarrow {BB'} .\overrightarrow {BA} \cr
& = - {{{a^2}} \over 2} + {{{a^2}} \over 2} = 0 \cr} \)
Vậy tứ giác A’B’CD là hình vuông.
Bài 3.15 trang 141 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD trong đó \(AB \bot AC,AB \bot B{\rm{D}}\). Gọi P và Q lần lượt là trung điểm của AB và CD. Chứng minh rằng AB và PQ vuông góc với nhau.
Giải:
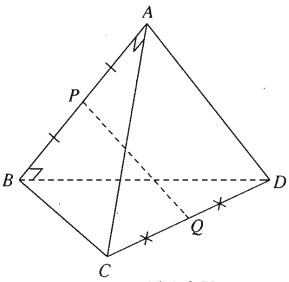
\(\eqalign{
& \overrightarrow {PQ} = \overrightarrow {PA} + \overrightarrow {AC} + \overrightarrow {CQ} \,\,\,\,\,\,\,\,\,\,\,\left( 1 \right) \cr
& \overrightarrow {PQ} = \overrightarrow {PB} + \overrightarrow {B{\rm{D}}} + \overrightarrow {DQ} \,\,\,\,\,\,\,\,\,\,\left( 2 \right) \cr} \)
Cộng từng vế (1) và (2) ta có:
\(2\overrightarrow {PQ} = \overrightarrow {AC} + \overrightarrow {B{\rm{D}}} \)
Suy ra \(2\overrightarrow {PQ} .\overrightarrow {AB} = \overrightarrow {AC} .\overrightarrow {AB} + \overrightarrow {B{\rm{D}}} .\overrightarrow {AB} = 0\)
Hay \(\overrightarrow {PQ} .\overrightarrow {AB} = 0\), tức là \(PQ \bot AB\).
congdong.edu.vn