Lớp 11 - SBT Toán học Giải bài 3.12, 3.13, 3.14 trang 170 Sách bài tập Đại số và giải tích 11
Bài 3.12 trang 170 Sách bài tập (SBT) Đại số và giải tích 11
Chứng minh phương trình
\({x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n} = 0\) luôn có nghiệm với n là số tự nhiên lẻ.
Giải:
Hàm số \(f\left( x \right) = {x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}\) xác định trên R
- Ta có
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {{x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}} \right) \cr
& {\rm{ = }}\mathop {\lim }\limits_{x \to + \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + ... + {{{a_{n - 1}}} \over {{x^{n - 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = + \infty \cr} \)
Vì \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to + \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = + \infty \)
Do đó, \(f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \(f\left( {{x_n}} \right) > 1\) kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại số a sao cho \(f\left( a \right) > 1\) (1)
\(\eqalign{
& \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left( {{x^n} + {a_1}{x^{n - 1}} + {a_2}{x^{n - 2}} + ... + {a_{n - 1}}x + {a_n}} \right) \cr
& {\rm{ = }}\mathop {\lim }\limits_{x \to - \infty } {x^n}\left( {1 + {{{a_1}} \over x} + {{{a_2}} \over {{x^2}}} + ... + {{{a_{n - 1}}} \over {{x^{n - 1}}}} + {{{a_n}} \over {{x^n}}}} \right) = - \infty \cr} \) (do n lẻ).
Vì \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - \infty\) nên với dãy số \(\left( {{x_n}} \right)\) bất kì mà \({x_n} \to - \infty \) ta luôn có \(\lim f\left( {{x_n}} \right) = - \infty \) hay \(\lim \left[ { - f\left( {{x_n}} \right)} \right] = + \infty \)
Do đó, \( - f\left( {{x_n}} \right)\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \( - f\left( {{x_n}} \right) > 1\) kể từ số hạng nào đó trở đi. Nói cách khác, luôn tồn tại b sao cho \( - f\left( b \right) > 1\) hay \(f\left( b \right) < - 1\) (2)
- Từ (1) và (2) suy ra \(f\left( a \right)f\left( b \right) < 0\)
Mặt khác, \(f\left( x \right)\) hàm đa thức liên tục trên R nên liên tục trên [a; b]
Do đó, phương trình \(f\left( x \right) = 0\) luôn có nghiệm.
Bài 3.13 trang 170 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn [a; b]. Nếu \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b)?Cho ví dụ minh hoạ.
Giải:
Nếu hàm số \(y = f\left( x \right)\) liên tục trên đoạn [a; b] và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Ví dụ minh hoạ :
- \(f\left( x \right) = {x^2} - 1\) liên tục trên đoạn \(\left[ { - 2;2} \right],f\left( { - 2} \right)f\left( 2 \right) = 9 > 0\)
Phương trình \({x^2} - 1 = 0\) có nghiệm \(x = \pm 1\) trong khoảng (-2; 2)
- \(f\left( x \right) = {x^2} + 1\) liên tục trên đoạn [-1; 1] và \(f\left( { - 1} \right)f\left( 1 \right) = 4 > 0\). Còn phương trình \({x^2} + 1 = 0\) lại vô nghiệm trong khoảng (-1; 1)
Bài 3.14 trang 170 Sách bài tập (SBT) Đại số và giải tích 11
Nếu hàm số \(y = f\left( x \right)\) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có nghiệm hay không trong khoảng (a; b) ?Hãy giải thích câu trả lời bằng minh hoạ hình học.
Giải:
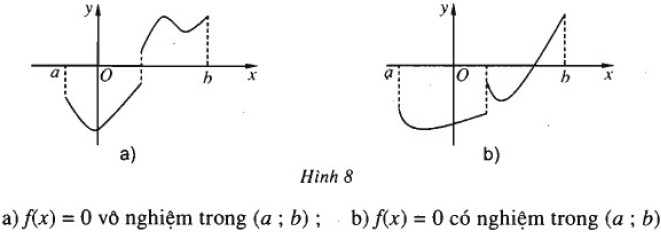
Nếu hàm số \(y = f\left( x \right)\) không liên tục trên đoạn [a; b] nhưng \(f\left( a \right)f\left( b \right) < 0\ thì phương trình \(f\left( x \right) = 0\) có thể có nghiệm hoặc vô nghiệm trong khoảng (a; b)
Minh hoạ hình hoạ (H.8):
congdong.edu.vn