Lớp 11 - SBT Toán học Giải bài 3.1, 3.2, 3.3, 3.4 trang 168 Sách bài tập Đại số và giải tích 11
Bài 3.1 trang 168 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số \(f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x}\)
Vẽ đồ thị của hàm số này. Từ đồ thị dự đoán các khoảng trên đó hàm số liên tục và chứng minh dự đoán đó.
Giải:
a)
\(f\left( x \right) = {{\left( {x - 1} \right)\left| x \right|} \over x} = \left\{ \matrix{
x - 1,\,{\rm{ nếu }}\,\,x > 0 \hfill \cr
1 - x,\,{\rm{ nếu\,\, x < 0}} \hfill \cr} \right.\) Hàm số này có tập xác định là \(R\backslash \left\{ 0 \right\}\)
b)
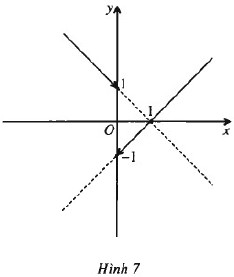
Từ đồ thị (H.7) dự đoán \(f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right),\;\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\) nhưng không liên tục trên R. Thật vậy,
- Với \(x > 0,f\left( x \right) = x - 1\) là hàm đa thức nên liên tục trên R do đó liên tục trên \(\left( {0{\rm{ }};{\rm{ }} + \infty } \right)\)
- Với \(x < 0,f\left( x \right) = 1 - x\) cũng làhàmđa thức nên liên tục trên R do đó liên tục trên \(\left( { - \infty {\rm{ }};{\rm{ }}0} \right)\)
Dễ thấy hàm số gián đoạn tại x = 0 vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = - 1,{\rm{ }}\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = 1\)
Bài 3.2 trang 168 Sách bài tập (SBT) Đại số và giải tích 11
Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c)
Giải:
Xét hàm số
\(f\left( x \right) = \left\{ \matrix{
x + 2,\,{\rm{nếu}} \le {\rm{0}} \hfill \cr
{1 \over {{x^2}}}{\rm\,{,nếu }}\,\,x > 0 \hfill \cr} \right.\)
- Trường hợp \(x \le 0\)
\(f\left( x \right) = x + 2\) là hàmđa thức, liên tục trên R nên nó liên tục trên (-2; 0]
- Trường hợp x > 0
\(f\left( x \right) = {1 \over {{x^2}}}\) là hàm số phân thức hữu tỉ nên liên tục trên (2; 0) thuộc tập xác định của nó.
Như vậy \(f\left( x \right)\) liên tục trên (-2; 0] và trên (0; 2)
Tuy nhiên, vì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {1 \over {{x^2}}} = + \infty \) nên hàm số \(f\left( x \right)\) không cógiới hạn hữu hạn tại x = 0. Do đó, nó không liên tục tại x = 0. Nghĩa là không liên tục trên (-2; 2)
Bài 3.3 trang 169 Sách bài tập (SBT) Đại số và giải tích 11
Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c)
Giải:
Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và \(\mathop {\lim }\limits_{x \to {b^ - }} f\left( x \right) = f\left( b \right)\) (1)
Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và \(\mathop {\lim }\limits_{x \to {b^ + }} f\left( x \right) = f\left( b \right)\) (2)
Từ (1) và (2) suy ra \(f\left( x \right)\) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b (vì \(\mathop {\lim }\limits_{x \to b} f\left( x \right) = f\left( b \right)\) ). Nghĩa là nó liên tục trên (a; c)
Bài 3.4 trang 169 Sách bài tập (SBT) Đại số và giải tích 11
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng (a; b) chứa điểm x0
Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} = L\) thì hàm số \(f\left( x \right)\) liên tục tại điểm x0
Hướng dẫn: Đặt \(g\left( x \right) = {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} - L\) và biểu diễn \(f\left( x \right)\) qua \(g\left( x \right)\)
Giải:
Đặt \(g\left( x \right) = {{f\left( x \right) - f\left( {{x_0}} \right)} \over {x - {x_0}}} - L\)
Suy ra \(g\left( x \right)\) xác định trên \(\left( {a{\rm{ }};{\rm{ }}b} \right)\backslash \left\{ {{x_0}} \right\}\) và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\)
Mặt khác, \(f\left( x \right) = f\left( {{x_0}} \right) + L\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)\) nên
\(\eqalign{
& \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( {{x_0}} \right) + L\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)} \right] \cr
& = \mathop {\lim }\limits_{x \to {x_0}} f\left( {{x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} L\left( {x - {x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} \left( {x - {x_0}} \right).\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = f\left( {{x_0}} \right). \cr} \)
Vậy hàm số \(y = f\left( x \right)\) liên tục tại
congdong.edu.vn