Lớp 11 - SBT Toán học Giải bài 1.43, 1.44, 1.45, 1.46 trang 40 Sách bài tập Hình học 11
Bài 1.43 trang 40 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy cho đường thẳng \(d:2x - y + 6 = 0\). Viết phương trình đường thẳng d’ là ảnh của d qua phép đối xứng tâm \(I\left( { - 2;1} \right)\).
Giải:
Dùng công thức tọa độ của phép đối xứng tâm \(I\left( { - 2;1} \right)\), ta có:
\(M' = {D_1}\left( M \right)\)
\(\Rightarrow M'\left\{ \matrix{
x' = 2.\left( { - 2} \right) - x \hfill \cr
y' = 2.1 - y \hfill \cr} \right.\)
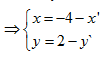
Thế \(\left( {x;y} \right)\) vào phương trình d, ta có phương trình
\(\eqalign{
& d':2\left( { - 4 - x'} \right) - \left( {2 - y'} \right) + 6 = 0 \cr
& \Rightarrow d':2{\rm{x}}' - y' + 4 = 0 \cr} \). Đổi kí hiệu, ta có phương trình:
\(d':2{\rm{x}} - y + 4 = 0\)
Bài 1.44 trang 40 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy cho đường tròn \(\left( C \right):{x^2} + {y^2} + 2x - 4y - 11 = 0\). Tìm phép tịnh tiến biến (C) thành \(\left( {C'} \right):{\left( {x - 10} \right)^2} + {\left( {y + 5} \right)^2} = 16\)
Giải:
(C) có tâm \(I\left( { - 1;2} \right)\), bán kính R = 4. (C’) có tâm \(I'\left( {10; - 5} \right)\), bán kính R’ = 4. Vậy \(\left( {C'} \right) = {T_{\vec v}}\left( C \right),\overrightarrow v = \overrightarrow {II'} = \left( {11; - 7} \right)\).
Bài 1.45 trang 40 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy cho hai đường thẳng \(d:x - 5y + 7 = 0\) và \(d':5x - y - 13 = 0\). Tìm phép đối xứng qua trục biến d thành d’.
Giải:
Nhận xét d và d’ không song song nên phép đối xứng trục biến d thành d’ có trục là phân giác của góc tạo bởi d và d’. Phương trình các đường phân giác là:
\(\eqalign{
& {{\left| {x - 5y + 7} \right|} \over {\sqrt {26} }} = {{\left| {5{\rm{x}} - y - 13} \right|} \over {\sqrt {26} }} \cr
& \Leftrightarrow \left[ \matrix{
x + y - 5 = 0 \hfill \cr
x - y - 1 = 0 \hfill \cr} \right. \cr}\)
Bài 1.46 trang 40 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(3x - y - 3 = 0\).Viết phương trình đường thẳng \(d_1\) là ảnh của d qua phép dời hình có được bằng cách thực hiện liên tiếp phép đối xứng tâm \(I\left( { - 1;2} \right)\) và phép quay tâm O góc quay -90°.
Giải:
Giả sử \({M_1} = {D_I}\left( M \right)\) và \(M' = {Q_{\left( {O; - {{90}^0}} \right)}}\left( {{M_1}} \right)\). Ta có
\(\left\{ \matrix{
{x_1} = - 2 - x \hfill \cr
{y_1} = 4 - y \hfill \cr} \right.\)
\(\left\{ \matrix{
x' = {y_1} \hfill \cr
y' = - {x_1} \hfill \cr} \right. \Rightarrow \left\{ \matrix{
x' = 4 - y \hfill \cr
y' = 2 + x \hfill \cr} \right.\)
\( \Rightarrow \left\{ \matrix{
4 - x` \hfill \cr
x = - 2 + y` \hfill \cr} \right.\)
Thế \(\left( {x;y} \right)\) theo \(\left( {x';y'} \right)\) vào phương trình d ta có:
\(\eqalign{
& 3\left( {y' - 2} \right) - \left( {4 - x'} \right) - 3 = 0 \cr
& \Leftrightarrow x' + 3y' - 13 = 0 \cr} \)
Vậy phương trình d’ là \(x + 3y - 13 = 0\).
congdong.edu.vn