Bài 3.20 trang 147 Sách bài tập (SBT) Hình học 11
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
a) Chứng minh \(BC \bot A{\rm{D}}\)
b) Gọi AH là đường cao của tam giác ADI
Chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Giải:
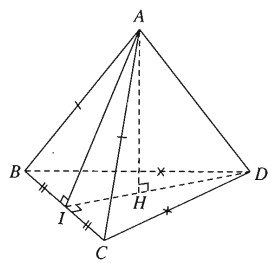
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên \(AI \bot BC\). Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên \(DI \bot BC\). Ta suy ra:
\(BC \bot \left( {AI{\rm{D}}} \right)\) nên \(BC \bot A{\rm{D}}\).
b) Vì \(BC \bot \left( {AI{\rm{D}}} \right)\) nên \(BC \bot AH\)
Mặt khác \(AH \bot I{\rm{D}}\) nên ta suy ra AH vuông góc với mặt phẳng (BCD).
Bài 3.21 trang 147 Sách bài tập (SBT) Hình học 11
Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.
Giải:
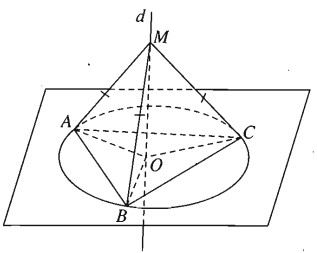
Phần thuận. Nếu MA = MB = MC nghĩa là M cách đều ba đỉnh của tam giác ABC và MO vuông góc với mặt phẳng (ABC) thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Từ đó ta suy ra OA = OB = OC nghĩa là A, B, C nằm trên đường tròn tâm O ngoại tiếp tam giác ABC. Vậy điểm M cách đều ba đỉnh của tam giác ABC thì nằm trên đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn ngoại tiếp tam giác ABC.
Phần đảo. Nếu ta lấy một điểm M bất kì thuộc đường thẳng d nói trên thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Do đó ta suy ra MA = MB = MC nghĩa là điểm M cách đều ba đỉnh của tam giác ABC.
Kết luận. Tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó. Người ta thường gọi đường thẳng d là trục của đường tròn (C).
congdong.edu.vn