Lớp 11 - SBT Toán học Giải bài 1.39, 1.40, 1.41, 1.42 trang 40 Sách bài tập Hình học 11
Bài 1.39 trang 40 Sách bài tập (SBT) Hình học 11
Gọi A', B', C' tương ứng là ảnh của ba điểm A, B, C qua phép đồng dạng tỉ số k. Chứng minh rằng: \(\overrightarrow {A'B'} .\overrightarrow {A'C'} = {k^2}\overrightarrow {AB.} \overrightarrow {AC} \)
Giải:
Theo định nghĩa của phép đồng dạng ta có \(B'C' = kBC\), từ đó suy ra \(B'C{'^2} = {k^2}B{C^2}\). Hay $${\left( {\overrightarrow {A'C'} - \overrightarrow {A'B'} } \right)^2} = {k^2}{\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right)^2}\). Suy ra
\(A'C{'^2} - 2\overrightarrow {A'C'} .\overrightarrow {A'B'} + A'B{'^2}\)
\(= {k^2}\left( {A{C^2} - 2\overrightarrow {AC} .\overrightarrow {AB} + A{B^2}} \right)\).
Để ý rằng \(A'C{'^2} = {k^2}A{C^2},A'B{'^2} = {k^2}A{B^2}\) ta suy ra điều phải chứng minh.
Bài 1.40 trang 40 Sách bài tập (SBT) Hình học 11
Gọi A’, B’ và C’ tương ứng là ảnh của ba điểmA, B và C qua phép đồng dạng. Chứng minh rằng \(\overrightarrow {AB} = p\overrightarrow {AC} \) nếu $$\overrightarrow {A'B'} = p\overrightarrow {A'C'} \) thì , trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.
Giải:
Để ý rằng
\(\eqalign{
& A'C{'^2} = {k^2}A{C^2},A'B{'^2} \cr
& = {k^2}A{B^2},\overrightarrow {A'C'} .\overrightarrow {A'B'} \cr
& = {k^2}\overrightarrow {AC} .\overrightarrow {AB} \cr} \)
Ta có:
\({\left( {\overrightarrow {A'B'} - p\overrightarrow {A'C'} } \right)^2} = A'B{'^2} - 2p\overrightarrow {A'B'} .\overrightarrow {A'C'} + {p^2}A'C{'^2}\)
\(\eqalign{
& = {k^2}\left( {A{B^2} - 2p\overrightarrow {AB} .\overrightarrow {AC} + {p^2}A{C^2}} \right) \cr
& = {k^2}{\left( {\overrightarrow {AB} - p\overleftarrow {AC} } \right)^2} = 0 \cr} \)
Từ đó suy ra \(\overrightarrow {A'B'} - p\overrightarrow {A'C'} = \overrightarrow 0 \)
Giả sử ba điểm \(A,B,C\) thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó \(\overrightarrow {AB} = t\overrightarrow {AC} \), với \(0 < t < 1\). Áp dụng bài 1.39 ta cũng có \(\overrightarrow {A'B} = t\overrightarrow {A'C'} \), với \(0 < t < 1\). Do đó ba điểm \(A',B',C'\) thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.
Bài 1.41 trang 40 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy xét phép biến hình F biến mỗi điểm \(M\left( {x;y} \right)\) thành \(M'\left( {2{\rm{x}} - 1; - 2y + 3} \right)\). Chứng minh F là một phép đồng dạng.
Giải:
Lấy điểm \(N\left( {{x_1};{y_1}} \right)\), thì điểm \(N'\left( {2{x_1} - 1; - 2{y_1} + 3} \right) = F\left( N \right)\). Ta có
\(\eqalign{
& M'N{'^2} = {\left( {2{{\rm{x}}_1} - 2{\rm{x}}} \right)^2} + {\left( { - 2{y_1} + 2y} \right)^2} \cr
& = 4\left[ {{{\left( {{x_1} - x} \right)}^2} + {{\left( {{y_1} - y} \right)}^2}} \right] = 4M{N^2} \cr} \)
Từ đó suy ra với hai điểm M, N tùy ý và M', N' lần lượt là ảnh của chúng qua F ta có \(M'N' = 2MN\). Vậy F là phép đồng dạng với tỉ số đồng dạng là 2.
Bài 1.42 trang 40 Sách bài tập (SBT) Hình học 11
Dựng tam giác BAC vuông cân tại A có C là một điểm cho trước, còn hai đỉnh A, B lần lượt thuộc hai đường thẳng a, b song song với nhau cho trước.
Giải:
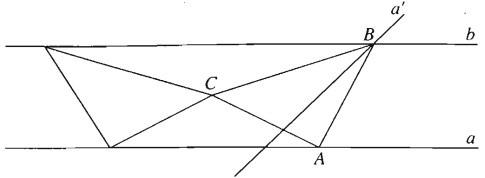
Xem B là ảnh của A qua phép đồng dạng có được bằng cách thực hiện liên tiếp phéo quay tâm C góc \( \pm {45^0}\) và phép vị tự tâm C tỉ số \(k = \sqrt 2 \). Vì A thuộc a nên B thuộc đường thẳng a’ là ảnh của a qua phép đồng dạng nói trên. Vậy b là giao của a’ và b. Từ đó suy ra cách dựng . Bài toán có hai nghiệm hình.
congdong.edu.vn