Lớp 11 - SBT Toán học Giải bài 1.35, 1.36, 1.37, 1.38 trang 39, 40 Sách bài tập Hình học 11
Bài 1.35 trang 39 Sách bài tập (SBT) Hình học 11
Cho đường tròn (C) và hai điểm cố định phân biệt A, B thuộc (C). Với mỗi điểm M chạy trên đường tròn (trừ hai điểm A, B), ta xét điểm N sao cho ABMN là hình bình hành. Chứng minh rằng tập hợp các điểm N cũng nằm trên một đường tròn xác định.
Giải:
Tập hợp các điểm N thuộc đường tròn (C') là ảnh của (C) qua phép đối xứng qua trung điểm của AB.
Bài 1.36 trang 39 Sách bài tập (SBT) Hình học 11
Cho hai đường tròn có cùng tâm O, bán kính lần lượt là R và \(r,\left( {R > r} \right)\). A là một điểm thuộc đường tròn bán kính r. Hãy dựng đường thẳng qua A cắt đường tròn bán kính r tại B, cắt đường tròn bán kính R tại C, D sao cho \(CD = 3AB\).
Giải:
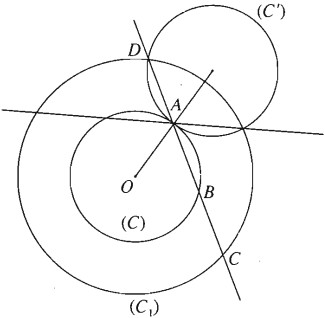
Gọi (C) là đường tròn tâm O bán kính r, \((C_1)\) là đường tròn tâm O bán kính R. Giả sử đường thẳng đã dựng được. Khi đó có thể xem D là ảnh của B qua phép đối xứng tâm A. Gọi (C') là ảnh của (C) qua phép đối xứng qua tâm A, thì D thuộc giao của (C') và \((C_1)\). Số nghiệm của bài toán phụ thuộc vào số giao điểm của (C') với \((C_1)\).
Bài 1.37 trang 39 Sách bài tập (SBT) Hình học 11
Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x + y - 2 = 0\). Hãy viết phương trình của đường thẳng d’ là ảnh của d qua phép quay tâm O góc 45°.
Giải:
Dễ thấy d chứa điểm \(H\left( {1;1} \right)\) và \(OH \bot d\). Gọi H' là ảnh của H qua phép quay tâm O góc 45° thì \(H' = \left( {0;\sqrt 2 } \right)\). Từ đó suy ra d' phải qua H' và vuông góc với OH'. Vậy phương trình của d' là \(y = \sqrt 2 \).
Bài 1.38 trang 40 Sách bài tập (SBT) Hình học 11
Qua tâm G của tam giác đều ABC, kẻ đường thẳng a cắt BC tại M và cắt AB tại N, kẻ đường thẳng b cắt AC tại P và AB tại Q, đồng thời góc giữa a và b bằng 60°. Chứng minh rằng tứ giác MNPQ là một hình thang cân.
Giải:
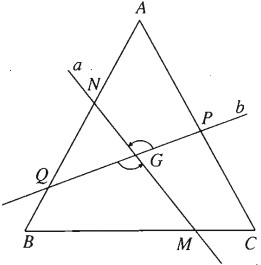
Gọi \({Q_{\left( {G;{{120}^0}} \right)}}\) là phép quay tâm G góc \(120^0\). Phép quay này biến b thành a, biến CA thành AB; do đó nó biến P thành N.
Tương tự \({Q_{\left( {G;{{120}^0}} \right)}}\) cũng biến Q thành M. Từ đó suy ra \(GP = GN,GQ = GM\). Do đó hai tam giác GNQ và GPM bằng nhau, suy ra NQ = PM. Vì \({Q_{\left( {G;{{120}^0}} \right)}}\) biến PQ thành NM nên \(PQ = NM\). Từ đó suy ra hai tam giác \(NQM\) và \(PMQ\) bằng nhau. Do đó \(\widehat {NQM} = \widehat {PMQ}\). Tương tự \(\widehat {QNP} = \widehat {MPN}\).
Từ đó suy ra \(\widehat {PNQ} + \widehat {NQM} = {180^0}\)
Do đó \(NP\parallel QM\). Vậy ta có tứ giác \(MPNQ\) là hình thang cân.
congdong.edu.vn