Bài 3.1 trang 131 Sách bài tập (SBT) Hình học 11
Cho hình lập phương ABCDA’B’C’D’ cạnh a. Gọi O và O’ theo thứ tự là tâm của hai hình vuông ABCD và A’B’C’D’.
a) Hãy biểu diễn các vectơ \(\overrightarrow {AO} ,\overrightarrow {AO'} \) theo các vectơ có điểm đầu và điểm cuối là các đỉnh của hình lập phương đã cho.
b) Chứng minh rằng \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB} \).
Giải:
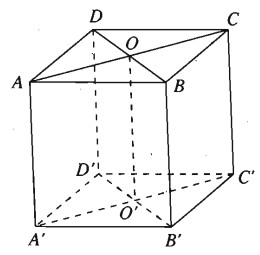
a) *\(\overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} = {1 \over 2}\overrightarrow {A'C'} = {1 \over 2}\left( {\overrightarrow {AB} + \overrightarrow {A{\rm{D}}} } \right)\)
\(\overrightarrow {AO} = \overrightarrow {AB} + \overrightarrow {BO} = \overrightarrow {AB} + {1 \over 2}\overrightarrow {B{\rm{D}}} ,v.v....\)
*\(\overrightarrow {AO} = {1 \over 2}\overrightarrow {AC} + \overrightarrow {AA'} \)
\(\eqalign{
& = {1 \over 2}\left( {\overrightarrow {AA'} + \overrightarrow {AC'} } \right) = {1 \over 2}\left( {\overrightarrow {AB'} + \overrightarrow {AD'} } \right) \cr
& = \overrightarrow {AA'} + \overrightarrow {A'B'} + {1 \over 2}\overrightarrow {B'D'} \cr
& = \overrightarrow {AB} + \overrightarrow {BB'} + {1 \over 2}\overrightarrow {B'D'} ,v.v... \cr} \)
b) \(\overrightarrow {AD} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AD} + \overrightarrow {DC} + \overrightarrow {CB} \)
(vì \(\overrightarrow {D'C'} = \overrightarrow {DC} \) và \(\overrightarrow {D'A'} = \overrightarrow {CB} \)) nên \(\overrightarrow {A{\rm{D}}} + \overrightarrow {D'C'} + \overrightarrow {D'A'} = \overrightarrow {AB} \).
Bài 3.2 trang 131 Sách bài tập (SBT) Hình học 11
Trong không gian cho điểm O và bốn điểm A, B, C, D phân biệt và không thẳng hàng. Chứng minh rằng điều kiện cần và đủ để bốn điểm A, B, C, D tạo thành một hình bình hành là:
\(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow {OB} + \overrightarrow {O{\rm{D}}} \)
Giải:
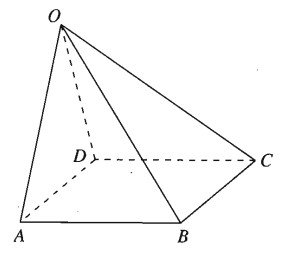
Giả sử bốn điểm A, B, C, D tạo thành một hình bình hành ta có:
\(\overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \) (với điểm O bất kì )
\( \Leftrightarrow \overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB} \)
Ngược lại, giả sử ta có hệ thức:
\(\overrightarrow {OC} + \overrightarrow {OA} = \overrightarrow {O{\rm{D}}} + \overrightarrow {OB} \)
\( \Leftrightarrow \overrightarrow {OC} - \overrightarrow {OB} = \overrightarrow {O{\rm{D}}} - \overrightarrow {OA} \)
\( \Leftrightarrow \overrightarrow {BC} = \overrightarrow {A{\rm{D}}} \)
Vì A, B, C, D không thẳng hàng nên tứ giác ABCD là hình bình hành.
Bài 3.3 trang 131 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD lần lượt ta lấy các điểm M, N sao cho
\({{AM} \over {AC}} = {{BN} \over {B{\rm{D}}}} = k\left( {k > 0} \right)\)
Chứng minh rằng ba vectơ \(\overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
Giải:
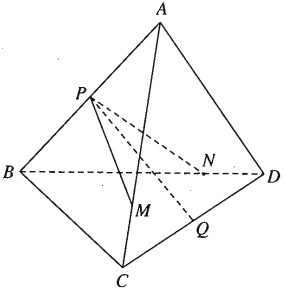
Ta có:
\(\eqalign{
& \overrightarrow {PQ} = {1 \over 2}\left( {\overrightarrow {PC} + \overrightarrow {P{\rm{D}}} } \right) \cr
& = {1 \over 2}\left[ {\left( {\overrightarrow {AC} - \overrightarrow {AP} } \right) + \left( {\overrightarrow {B{\rm{D}}} - \overrightarrow {BP} } \right)} \right] \cr
& = {1 \over 2}\left[ {\left( {\overrightarrow {AC} + \overrightarrow {B{\rm{D}}} } \right) - \underbrace {\left( {\overrightarrow {AP} + \overrightarrow {BP} } \right)}_{\overrightarrow 0 }} \right] \cr
& = {1 \over 2}.{1 \over k}\left( {\overrightarrow {AM} + \overrightarrow {BN} } \right) \cr} \)
Vì \(\overrightarrow {AC} = {1 \over k}.\overrightarrow {AM} \) và \(\overrightarrow {B{\rm{D}}} = {1 \over k}.\overrightarrow {BN} \)
Đồng thời \(\overrightarrow {AM} = \overrightarrow {AP} + \overrightarrow {PM} \) và \(\overrightarrow {BN} = \overrightarrow {BP} + \overrightarrow {PN} \), nên \(\overrightarrow {PQ} = {1 \over {2k}}\left( {\overrightarrow {PM} + \overrightarrow {PN} } \right)\) vì \(\overrightarrow {AP} + \overrightarrow {BP} = \overrightarrow 0 \)
Vậy \(\overrightarrow {PQ} = {1 \over {2k}}\overrightarrow {PM} + {1 \over {2k}}\overrightarrow {PN} \)
Do đó ba vectơ \(\overrightarrow {PQ} ,\overrightarrow {PM} ,\overrightarrow {PN} \) đồng phẳng.
congdong.edu.vn