Lớp 11 - SBT Toán học Giải bài 2.5, 2.6, 2.7, 2.8 trang 112 Sách bài tập Đại số và giải tích 11
Bài 2.5 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) với \(\left( {{u_n}} \right) = 1 + \left( {n - 1} \right){.2^n}\)
a) Viết năm số hạng đầu của dãy số ;
b) Tìm công thức truy hồi ;
c) Chứng minh (un) là dãy số tăng và bị chặn dưới.
Giải:
a) Học sinh tự giải.
b) HD: Tìm hiệu \({u_{n + 1}} - {u_n}\)
ĐS:
\(\left\{ \matrix{
{u_1} = 1 \hfill \cr
{u_{n + 1}} = {u_n} + \left( {n + 1} \right){2^n}{\rm\,\,{ với }}\,\,n \ge 1 \hfill \cr} \right.\)
c) HD: Xét dấu \({u_{n + 1}} - {u_n}\)
Bài 2.6 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Các dãy số (un), (vn)được xác định bằng công thức
a) \(\left\{ \matrix{
{u_1} = 1 \hfill \cr
{u_{n + 1}} = {u_n} + {n^3}{\rm{ voi }}n \ge 1; \hfill \cr} \right.\)
b) \(\left\{ \matrix{
{v_1} = 2 \hfill \cr
{v_{n + 1}} = v_n^2{\rm{ }}voi{\rm{ }}n \ge 1 \hfill \cr} \right.\)
Tìm công thức tính (un), (vn) theo n. Tính số hạng thứ 100 của dãy số (un). Hỏi số 4294967296 là số hạng thứ mấy của dãy số (vn)
Giải:
a) Từ \({u_{n + 1}} - {u_n} = {n^3}\) ta có
\(\eqalign{
& {u_1} = 1; \cr
& {u_2} - {u_1} = {1^3}; \cr
& {u_3} - {u_2} = {2^3}; \cr
& ... \cr
& {u_{n - 1}} - {u_{n - 2}} = {\left( {n - 2} \right)^3}; \cr
& {u_n} - {u_{n - 1}} = {\left( {n - 1} \right)^3}. \cr} \)
Cộng từng vế n đẳng thức trên và rút gọn, ta được
\({u_n} = 1 + {1^3} + {2^3} + ... + {\left( {n - 1} \right)^3}\)
Sử dụng kết quả bài tập 12 b) - ta có
\({1^3} + {2^3} + ... + {\left( {n - 1} \right)^3} = {{{{\left( {n - 1} \right)}^2}{n^2}} \over 4}\)
Vậy
\(\eqalign{
& {u_n} = 1 + {{{n^2}{{\left( {n - 1} \right)}^2}} \over 4}. \cr
& {u_{100}} = 24502501. \cr} \)
b) Hãy viết một vài số hạng đầu của dãy và quan sát
\(\eqalign{
& {v_1} = 2; \cr
& {v_2} = v_1^2 = {2^2}; \cr
& {v_3} = v_2^2 = {2^4} = {2^{{2^2}}}; \cr
& {v_4} = v_3^2 = {2^8} = {2^{{2^3}}} \cr} \)
Từ đây dự đoán \({v_n} = {2^{{2^{n - 1}}}}\)
Công thức trên dễ dàng chứng minh bằng phương pháp quy nạp. Số 4294967296 là số hạng thứ sáu của dãy số (vn)
Bài 2.7 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
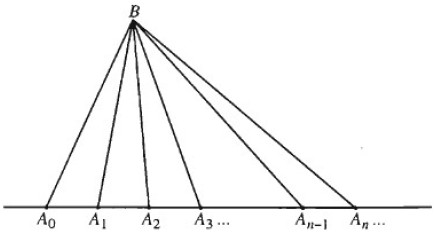
Dãy số \(\left( {{x_n}} \right)\) được biểu diễn trên trục số bởi tập hợp các điểm, kí hiệu là A :
$$A = \left\{ {{A_0},{A_1},{A_2},...,{A_n}} \right\}$$
Gọi B là điểm nằm ngoài trục số. Người ta dựng các tam giác đỉnh B và hai đỉnh còn lại thuộc tập hợp A.
Đặt un là số các tam giác được tạo thành từ B và hai trong số n + 1 điểm \({A_0},{A_1},{A_2},...,{A_n}\) rồi lập dãy số un
a) Tính \({u_1},{u_2},{u_3},{u_4}\) ;
b) Chứng minh rằng \({u_n} = C_{n + 1}^2\) và \9{u_{n + 1}} = {u_n} + n + 1\)
Giải:
a)
\(\eqalign{
& {u_1} = 1 \cr
& {u_2} = 3 \cr
& {u_3} = 6 \cr
& {u_4} = 10 \cr} \)
b) Số các tam giác un tạo thành từ B và n + 1 điểm chính là số tổ hợp chập 2 của n + 1 phần tử:
Áp dụng công thức \(C_n^k = C_{n - 1}^k + C_{n - 1}^{k - 1}\)
Ta có \(C_{n + 2}^2 = C_{n + 1}^2 + C_{n + 1}^1\)
Hay \({u_{n + 1}} = {u_n} + n + 1\)
Bài 2.8 trang 112 Sách bài tập (SBT) Đại số và giải tích 11
Cho dãy số (un) thoả mãn điều kiện: Với mọi n ∈ N* thì \(0 < {u_n} < 1\) và \({u_{n + 1}} < 1 - {1 \over {4{u_n}}}\)
Chứng minh dãy số đã cho là dãy giảm.
Giải:
Vì \(0 < {u_n} < 1\) với mọi n nên \(1 - {u_{n + 1}} > 0\).
Áp dụng bất đẳng thức Cô – si ta có \({u_{n + 1}}\left( {1 - {u_{n + 1}}} \right) \le {1 \over 4}\)
Mặt khác, từ giả thiết \({u_{n + 1}} < 1 - {1 \over {4{u_n}}}\)
suy ra \({u_{n + 1}}.{u_n} < {u_n} - {1 \over 4}\) hay \({1 \over 4} < {u_n}\left( {1 - {u_{n + 1}}} \right)\)
So sánh (1) và (2) ta có:
\({u_{n + 1}}\left( {1 - {u_{n + 1}}} \right) < {u_n}\left( {1 - {u_{n + 1}}} \right)\) hay \({u_{n + 1}} < {u_n}\)
congdong.edu.vn