Lớp 11 - SBT Toán học Giải bài 1.51, 1.52, 1.53 trang 41 Sách bài tập Hình học 11
Bài 1.51 trang 41 Sách bài tập (SBT) Hình học 11
Cho đường tròn (O, R) , gọi BC là dây cung cố định của đường tròn và A là một điểm di động trên đường tròn. Tìm tập hợp trực tâm H của tam giác ABC.
Giải:
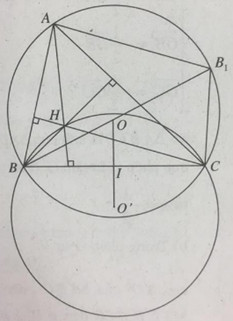
Vẽ đường kính BB1. Vì \(A{B_1}\parallel HC\) và \(AH\parallel {B_1}C\) nên AHCB1 là hình bình hành, suy ra: \(\overrightarrow {AH} = \overrightarrow {{B_1}C} \). B, C cố định nên \(\overrightarrow {{B_1}C} \) không đổi.
Như vậy \(H = {T_{\overrightarrow {{B_1}C} }}\left( A \right)\). Suy ra tập hợp các điểm H là đường tròn \(C'\left( {O';R} \right)\), chính là ảnh của đường tròn \(C\left( {O;R} \right)\) qua phép tịnh tiến \({T_{\overrightarrow {{B_1}C} }}\).
+ Xác định tâm của (C’):
Ta có:
\(O' = {T_{\overrightarrow {{B_1}C} }}\left( O \right),\overrightarrow {OO'} = \overrightarrow {{B_1}C} = 2\overrightarrow {OI} \)
(I là trung điểm của BC). Vậy O’ đối xứng với O qua BC.
Bài 1.52 trang 41 Sách bài tập (SBT) Hình học 11
Cho tam giác đều ABC và điểm P nằm trong tam giác, sao cho PC = 3, PA = 4 và PB = 5. Tìm chu vi của tam giác ABC.
Giải:
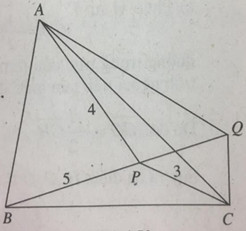
Xét phép quay \({Q_{\left( {C,{{60}^0}} \right)}}:\Delta CBP \mapsto \Delta CAQ\).
Ta có :
\(\left\{ \matrix{
CP = CQ \hfill \cr
\widehat {PCQ} = {60^0} \hfill \cr} \right. \Rightarrow \Delta PCQ\) là tam giác đều.
\(\left\{ \matrix{
AQ = BP = 5 \hfill \cr
AP = 4 \hfill \cr
PQ = PC = 3 \hfill \cr} \right. \Rightarrow A{Q^2} = A{P^2} + P{Q^2}\)
\( \Rightarrow \widehat {APQ} = {90^0}\)
\(\widehat {APC} = \widehat {APQ} + \widehat {QPC} = {90^0} + {60^0} = {150^0}\)
Áp dụng định lí hàm số côsin trong tam giác APC ta tính được chu vi tam giác ABC là: \(p = 3{\rm{A}}C = 3\sqrt {25 + 12\sqrt 3 } \)
Bài 1.53 trang 41 Sách bài tập (SBT) Hình học 11
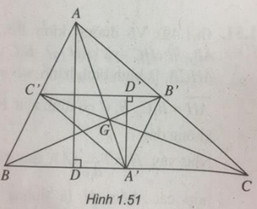
Cho tam giác ABC. Các trung tuyến AA',BB', CC' cắt nhau tại G.
a) Chứng minh rằng tam giác A'B'C' là ảnh của tam giác ABC qua phép vị tự tỉ số k xác định.
b) Kẻ đường cao xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng ảnh của đường cao này qua phép vị tự \({V_{\left( {G,k} \right)}}\) là đường trung trực của đoạn thẳng BC
c) Gọi H là trực tâm của tam giác ABC và O là tâm đường tròn ngoại tiếp tam giác ABC. Chứng minh rằng phép vị tự \({V_{\left( {G,k} \right)}}\) nói trên biến điểm H thành điểm O. Suy ra rằng ba điểm H, G, O nằm trên một đường thẳng ( đường thẳng Ơ-le của tam giác).
Giải:
\(\left\{ \matrix{
\overrightarrow {GA'} = - {1 \over 2}\overrightarrow {GA} \hfill \cr
\overrightarrow {GB'} = - {1 \over 2}\overrightarrow {GB} \hfill \cr
\overrightarrow {GC'} = - {1 \over 2}\overrightarrow {GC} \hfill \cr} \right.\)
⇒ ∆A’B’C’ là ảnh của ∆ABC qua phép vị tự tâm G, tỉ số vị tự \(k = - {1 \over 2}\)
b) Trong phép vị tự \({V_{\left( {G,k = - {1 \over 2}} \right)}}\), đường cao AD của ∆ABC biến thành đường cao A’D’ của ∆A’B’C’, nên \(A'D' \bot C'B'\).
Mà \(C'B'\parallel CB\) nên .
Mặt khác A’ là trung điểm của đoạn thẳng BC.
Suy ra A’D’ là đường trung trực của đoạn thẳng BC.
c) Phép vị tự \({V_{\left( {G,k = - {1 \over 2}} \right)}}\) biến các đường cao của tam giác ABC thành các đường trung trực của tam giácABC nên trực tâm H biến thành tâm O đường tròn ngoại tiếp tam giác ABC.
Do đó : \(\overrightarrow {GO} = - {1 \over 2}\overrightarrow {GH} \)
Suy ra ba điểm H, G, O thẳng hàng.
congdong.edu.vn