Lớp 11 - SBT Toán học Giải bài 3.22, 3.23, 3.24 trang 152 Sách bài tập Hình học 11
Bài 3.22 trang 152 Sách bài tập (SBT) Hình học 11
Hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng nhau. Chứng minh rằng \(AC \bot B'D',AB' \bot C{\rm{D}}'\) và \(A{\rm{D}}' \bot CB'\). Khi mặt phẳng (AA’C’C) vuông góc với mặt phẳng (BB’D’D)?
Giải:
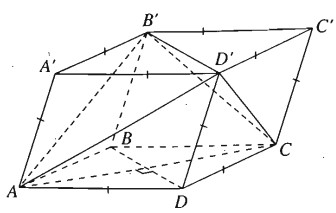
Theo giả thiết các mặt của hình hộp đều là hình thoi.
Ta có ABCD là hình thoi nên \(AC \bot B{\rm{D}}\)
Theo tính chất của hình hộp: \(B{\rm{D}}\parallel B'D'\),do đó \(AC \bot B'{\rm{D'}}\).
Chứng minh tương tự ta được \(AB' \bot C{\rm{D', AD}}' \bot CB'\)
Hai mặt phẳng (AA’C’C) và (BB’D’D) vuông góc với nhau khi hình hộp ABCD.A’B’C’D’là hình lập phương.
Bài 3.23 trang 152 Sách bài tập (SBT) Hình học 11
Cho tứ diện ABCD có ba cặp cạnh đối diện bằng nhau là AB = CD, AC = BD và AD = BC. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng minh \(MN \bot AB\) và \(MN \bot C{\rm{D}}\). Mặt phẳng (CDM) có vuông góc với mặt phẳng (ABN) không? Vì sao?
Giải:
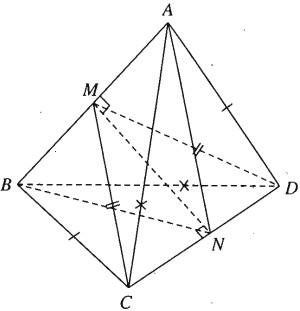
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó \(MN \bot C{\rm{D}}\) vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra \(MN \bot AB\). Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.
Bài 3.24 trang 152 Sách bài tập (SBT) Hình học 11
Chứng minh rằng nếu tứ diện ABCD có \(AB \bot C{\rm{D}}\) và \(AC \bot B{\rm{D}}\) thì \(AD \bot BC\).
Giải:
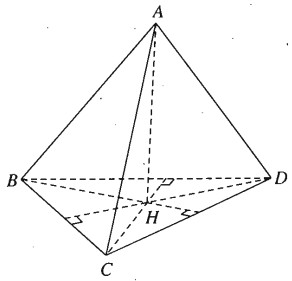
Vẽ \(AH \bot \left( {BC{\rm{D}}} \right)\) tại H, ta có \(C{\rm{D}} \bot AH\) và vì \(C{\rm{D}} \bot AB\) ta suy ra \(C{\rm{D}} \bot BH\). Tương tự vì \({\rm{BD}} \bot AC\) ta suy ra \({\rm{BD}} \bot CH\)
Vậy H là trực tâm của tam giác BCD tức là \(DH \bot BC\)
Vì \(AH \bot BC\) nên ta suy ra \(BC \bot A{\rm{D}}\)
Cách khác . Trước hết ta hãy chứng minh hệ thức:
\(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = 0\) với bốn điểm A, B, C, D bất kì.
Thực vậy , ta có:
\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = \overrightarrow {AB} .\left( {\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {{\rm{AD}}} - \overrightarrow {AC} .\overrightarrow {AB} \,\,\,\,\,\,\,\left( 1 \right) \cr
& \overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} .\left( {\overrightarrow {AB} - \overrightarrow {{\rm{AD}}} } \right) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {{\rm{AD}}} \,\,\,\,\,\,\left( 2 \right) \cr
& \overrightarrow {{\rm{AD}}} .\overrightarrow {BC} = \overrightarrow {{\rm{AD}}} .\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \overrightarrow {{\rm{AD}}} .\overrightarrow {AC} - \overrightarrow {{\rm{AD}}} .\overrightarrow {AB} \,\,\,\,\,\,\,\left( 3 \right) \cr} \)
\(\left( 1 \right) + \left( 2 \right) + \left( 3 \right) \Leftrightarrow \overrightarrow {AB} .\overrightarrow {C{\rm{D}}} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\,\,\,\,\,\,\left( 4 \right)\)
Do đó nếu \(AB \bot CD\) nghĩa là \(\overrightarrow {AB} .\overrightarrow {C{\rm{D}}} = 0\,\,\), \(AC \bot BD\) nghĩa là \(\overrightarrow {AC} .\overrightarrow {B{\rm{D}}} = 0\,\,\)
Từ hệ thức (4) ta suy ra \(\overrightarrow {AD} .\overrightarrow {BC} = 0\,\,\), do đó \(A{\rm{D}} \bot BC\).
Bài 3.25 trang 152 Sách bài tập (SBT) Hình học 11
Cho tam giác ABC vuông tại B. Một đoạn thẳng AD vuông góc với mặt phẳng (ABC). Chứng minh rằng mặt phẳng (ABD) vuông góc với mặt phẳng (BCD).
Từ điểm A trong mặt phẳng (ABD) ta vẽ AH vuông góc với BD, chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Giải:
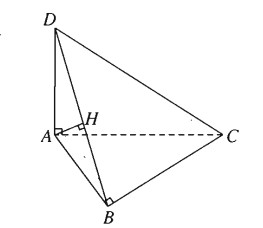
Vì \(A{\rm{D}} \bot \left( {ABC} \right)\) nên \(A{\rm{D}} \bot BC\)
Ngoài ra \(BC \bot AB\) nên ta có \(BC \bot \left( {ABD} \right)\)
Vì mặt phẳng (BCD) chứa BC mà \(BC \bot \left( {ABD} \right)\) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD. Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).
congdong.edu.vn