ĐỀ 1
Câu 1 trang 224 sách bài tập (SBT) – Giải tích 12 (4 điểm)
Cho hàm số \(y = 2 - {2 \over {x - 2}}\)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Từ (C) vẽ đồ thị của hàm số \(y = |{{2(x - 3)} \over {x - 2}}|\) (1)
Dựa vào đồ thị (1), hãy biện luận theo k số nghiệm của phương trình \(|{{2(x - 3)} \over {x - 2}}| = {\log _2}k\) (2)
3) Tìm các điểm thuộc (C) có tọa độ nguyên.
Hướng dẫn làm bài
1) Vẽ đồ thị hàm số
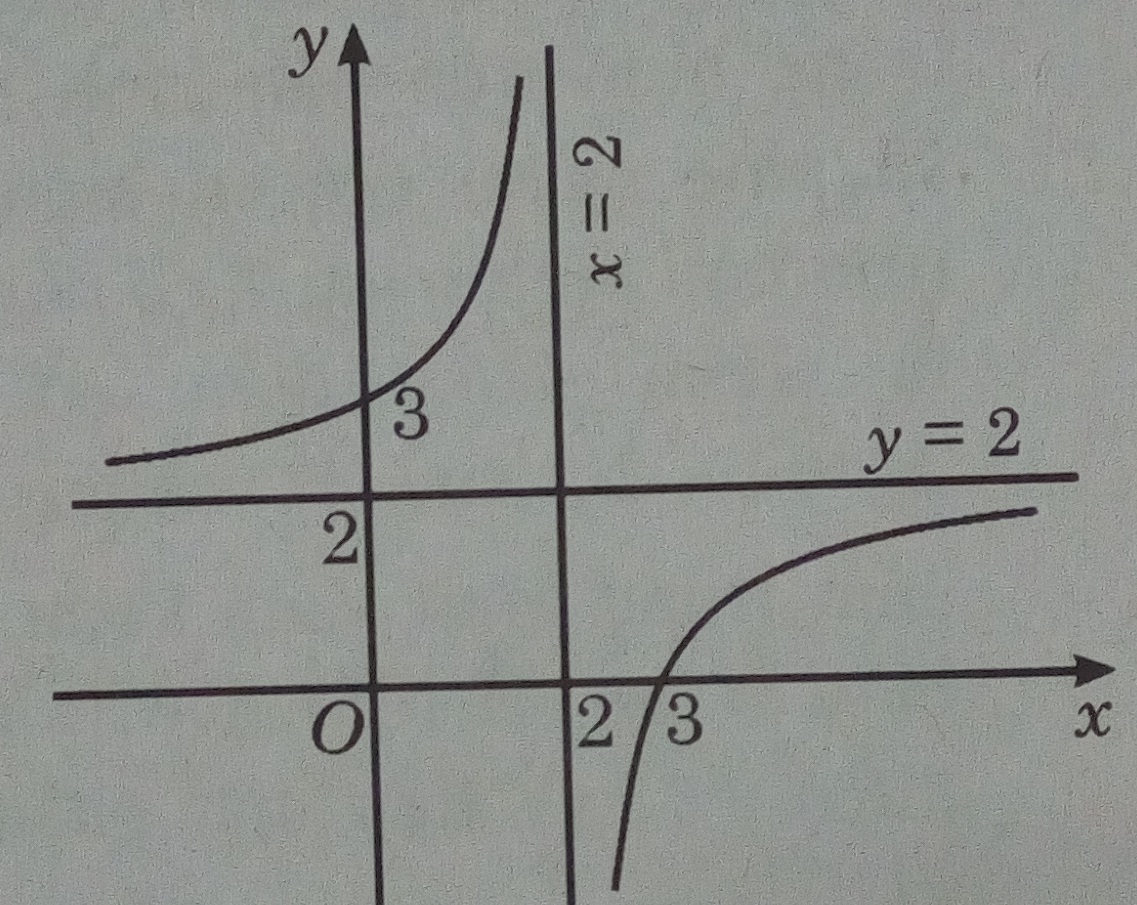
2) Đồ thị của (1) được suy ra từ đồ thị (C) bằng cách giữ nguyên phần đồ thị nằm phía trên trục hoành và lấy đối xứng qua trục hoành phần đồ thị nằm phía dưới trục hoành
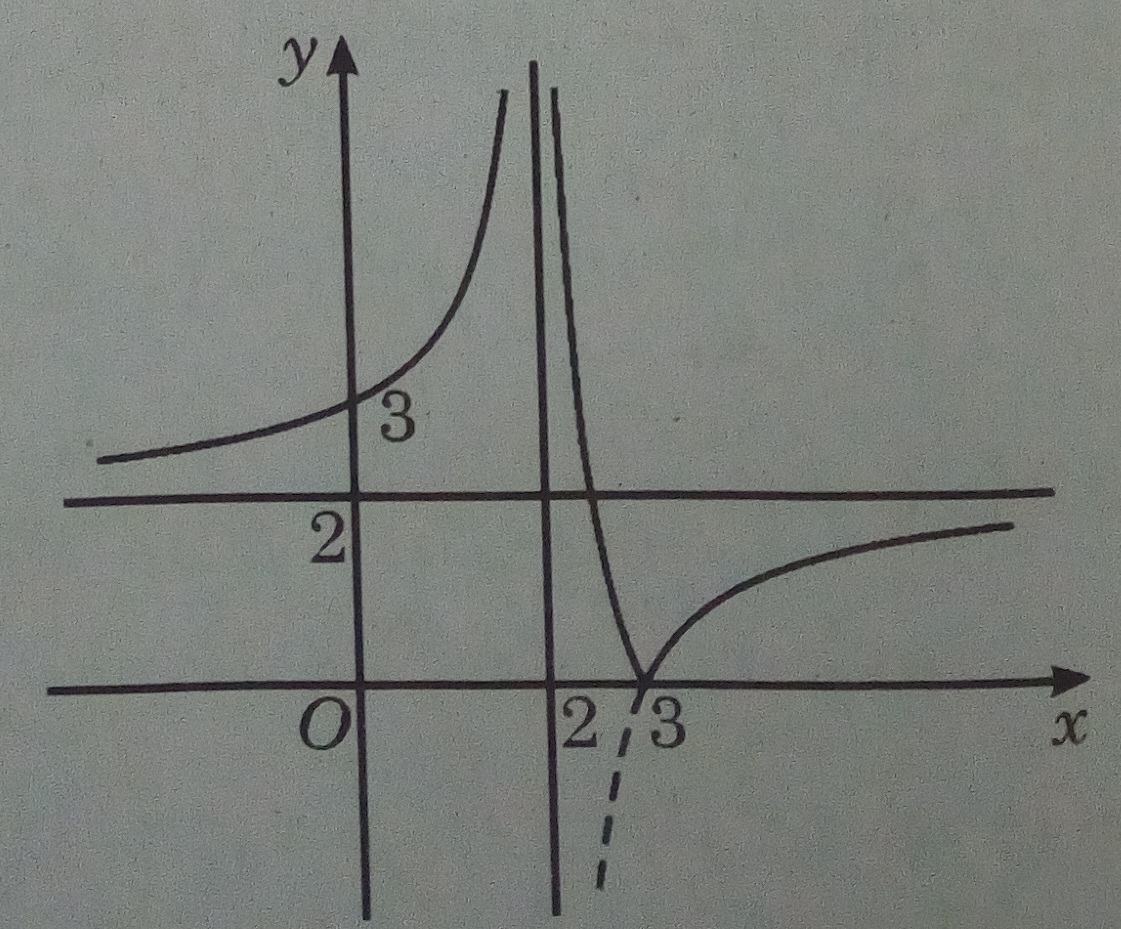
Số nghiệm của (2) là số giao điểm của đồ thị (1) với đường thẳng \(y = {\log _2}k\)
Dựa trên đồ thị, ta suy ra:
* Phương trình (2) vô nghiệm nếu
\( - \infty < {\log _2}k < 0 \Leftrightarrow < k < 1\)
* Phương trình (2) có một nghiệm nếu \({\log _2}k = 0\) hoặc \({\log _2}k = 2\) , tức là khi k = 1 hoặc k = 4.
* Phương trình (2) có hai nghiệm nếu \(0 < {\log _2}k < 2\) hoặc \({\log _2}k > 2\) , tức là khi 1 < k < 4 hoặc k > 4.
Kết luận: Phương trình vô nghiệm khi 0 < k < 1 ;
Phương trình có một nghiệm khi k = 1 hoặc k = 4 ;
Phương trình có hai nghiệm khi 1 < k < 4 hoặc k > 4.
3) Ta có \(y = 2 - {2 \over {x - 2}}\) nên y nguyên khi và chỉ khi x – 2 là ước của 2, tức là \(x - 2 = \pm 1\) hoặc \(x - 2 = \pm 2\) . Từ đó, ta có các điểm có tọa độ nguyên là (3; 0), (1; 4), (4; 1) và (0; 3).
Câu 2 trang 224 sách bài tập (SBT) – Giải tích 12 (3 điểm)
Giải các phương trình sau:
1) \({32^{{{x + 5} \over {x - 7}}}} = 0,{25.128^{{{x + 17} \over {x - 3}}}}\)
2) \({\log _2}(\cot x + \tan 3x) - 1 = {\log _2}(\tan 3x)\)
Hướng dẫn làm bài
1) Vì \(32 = {2^5};0,25 = {1 \over 4} = {2^{ - 2}};128 = {2^7}\) , nên phương trình đã cho tương đương với:
\({2^{{{5(x + 5)} \over {x - 7}}}} = {2^{{{7(x + 17)} \over {x - 3}} - 2}} \Leftrightarrow {{5x + 25} \over {x - 7}} = {{5x + 125} \over {x - 3}} \Leftrightarrow x = 10\) (thỏa mãn điều kiện \(x \ne 7,x \ne 3\) )
2) Điều kiện
\(\left\{ {\matrix{{\cot x + \tan 3x > 0} \cr {\tan 3x > 0} \cr} } \right.\)
Phương trình đã cho tương đương với \(\cot x + \tan 3x = 2\tan 3x\)
\(\Leftrightarrow \cot x = \tan 3x\) (*)
\(\Leftrightarrow 3x = {\pi \over 2} - x + k\pi \Leftrightarrow x = {\pi \over 8} + {{k\pi } \over 4},k \in Z\)
Để chọn những góc thỏa mãn điều kiện, trước hết từ (*) suy ra và phải cùng dấu với nhau.
Lần lượt cho k = 0, 1, 2, ……,7, ta chọn được những góc không thỏa mãn điều kiện.
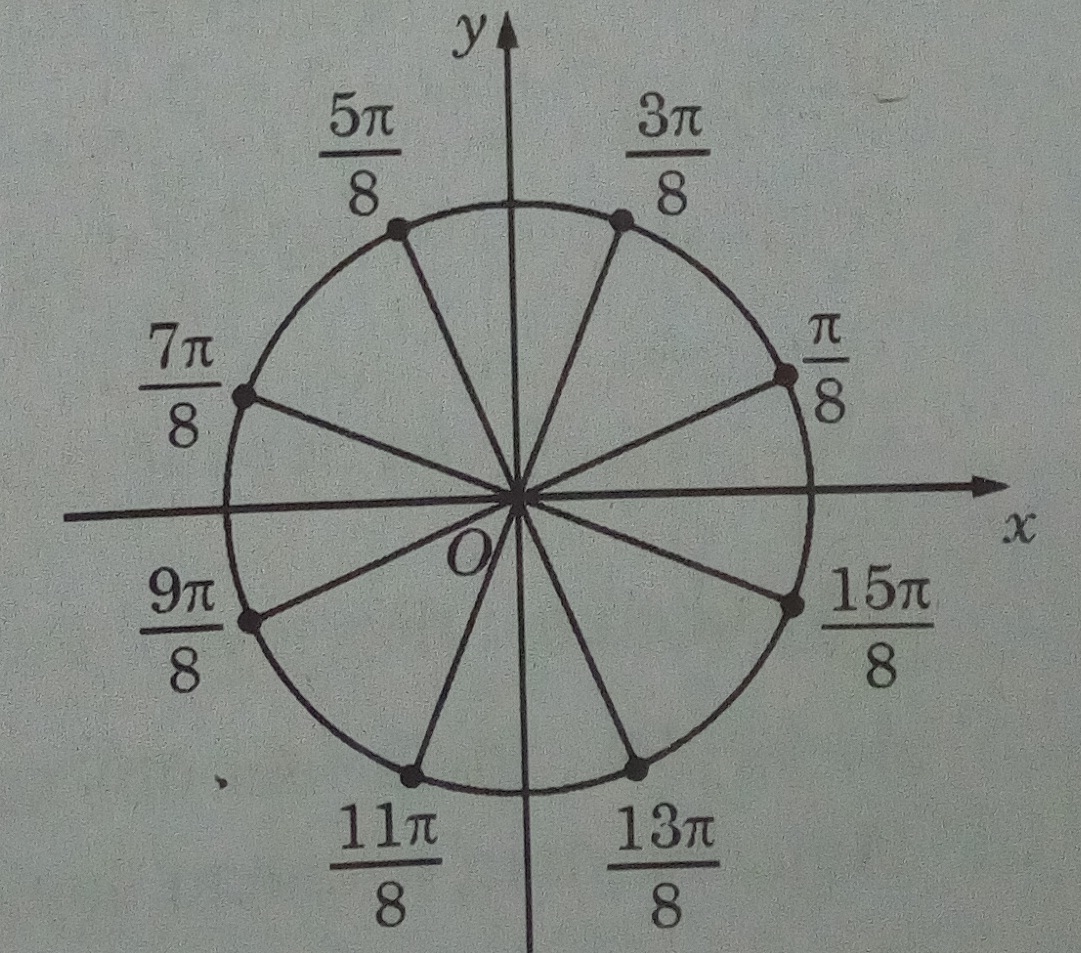
Khi đó, nghiệm của phương trình đã cho là \(x = {\pi \over 8} + k\pi \) và \(x = {{3\pi } \over 8} + k\pi ,k \in Z\)
Câu 3 trang 224 sách bài tập (SBT) – Giải tích 12 (3 điểm)
1) Tính tích phân \(\int\limits_0^2 {\sqrt {1 + 2{x^2}} xdx} \) (đặt \(t = \sqrt {1 + 2{x^2}} \))
2) Tìm modun của số phức \(z = {{ - 8 - 3i} \over {1 - i}}\)
Hướng dẫn làm bài
a) Đổi biến: \(t = \sqrt {1 + 2{x^2}}\Rightarrow {t^2} = 1 + 2{x^2}\)
\(\Rightarrow 2tdt = 4xdx = > xdx = {{tdt} \over 2}\)
Và \(x = 0 \Rightarrow t = 1 ; x = 2\Rightarrow t = 3.\)
Vậy \(\int\limits_0^2 {\sqrt {1 + 2{x^2}} } dx = {1 \over 2}\int\limits_1^3 {{t^2}dt = {1 \over 6}{t^3}\left| {\matrix{3 \cr 1 \cr} } \right.} = 4{1 \over 3}\)
b) Áp dụng công thức \(|z| = {{|{z_1}|} \over {|{z_2}|}}\) . Đáp số: \(|z| = {{\sqrt {146} } \over 2}\)
ĐỀ 2.
Câu 1 trang 225 sách bài tập (SBT) – Giải tích 12 (4,5 điểm)
Cho hàm số \(y = - {1 \over 3}{x^3} + {x^2} + m - 1\)
1) Chứng minh rằng đồ thị của hàm số đã cho luôn có hai điểm cực trị. Xác định m để một trong những điểm cực trị đó thuộc trục Ox.
2) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi \(m = {1 \over 3}\)
3) Viết phương trình tiếp tuyến với (C) , biết rằng tiếp tuyến đó vuông góc với đường thẳng \(y = {1 \over 3}x - 2\)
4) Tính diện tích hình phẳng giới hạn bởi (C) , trục hoành và hai đường thẳng x = 0 và x = 2.
Hướng dẫn làm bài
1) \(y' = - {x^2} + 2x;y' = 0 \Leftrightarrow \left[ {\matrix{{x = 0} \cr {x = 2} \cr} } \right.\)
Ta có y’ > 0 với \(x \in (0;2)\) và y’ < 0 khi x thuộc các khoảng \(( - \infty ;0),(2; + \infty )\). Vậy với mọi m, đồ thị của hàm số luôn có điểm cực tiểu (0; m – 1) và điểm cực đại \((2;m + {1 \over 3})\). Một trong các điểm cực trị nằm trên trục Ox khi và chỉ khi hoặc \(m + {1 \over 3} = 0 \Leftrightarrow m = - {1 \over 3}\) hoặc \(m – 1 = 0 \Leftrightarrow m = 1.\)
2) Với \(m = {1 \over 3}\) , ta có \(y = - {1 \over 3}{x^3} + {x^2} - {2 \over 3}\)
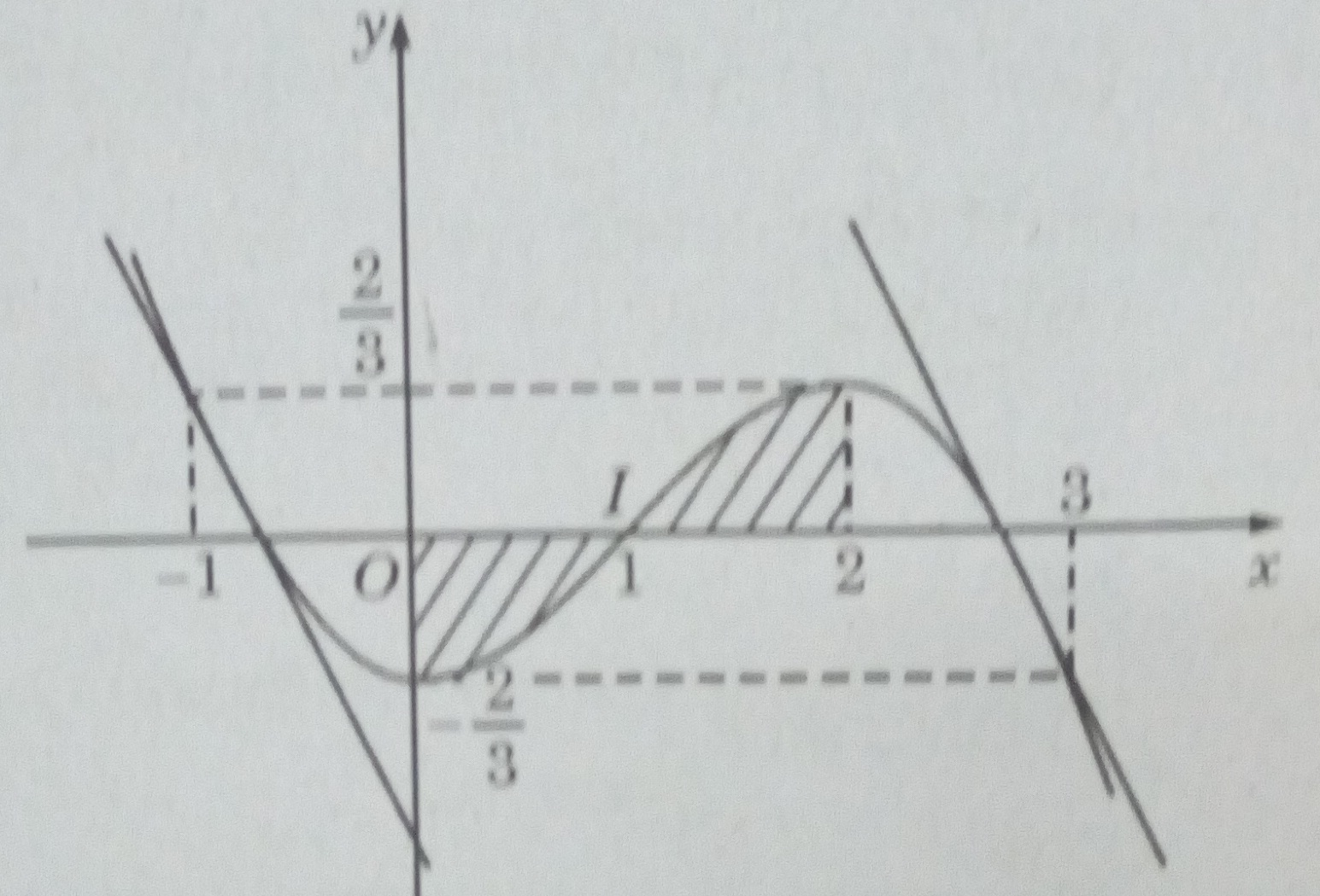
3) Hệ số góc của tiếp tuyến là -3. Hoành độ tiếp điểm thỏa mãn phương trình
\( - {\rm{ }}{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\Rightarrow \left[ {\matrix{{{x_1} = - 1} \cr {{x_2} = 3} \cr} } \right.\)
Các tung độ của tiếp điểm tương ứng là \({y_1} = {2 \over 3};{y_2} = - {2 \over 3}\)
Vậy ta có hai tiếp tuyến \(y = - 3x - {7 \over 3}\) và \(y = - 3x + {{25} \over 3}\)
4) Vì I(1; 0) là tâm đối xứng của (C) nên hình phẳng đã cho gồm hai hình đối xứng với nhau qua điểm I (1; 0) . Vậy : \(S = 2\int\limits_0^1 {({1 \over 3}{x^3} - {x^2} + {2 \over 3})dx = {5 \over 6}} \) (đơn vị thể tích)
Câu 2 trang 225 sách bài tập (SBT) – Giải tích 12 (3 điểm)
1) Giải phương trình \({3^{{x \over 5}}} + {3^{{{x - 10} \over {10}}}} = 84\)
2) Giải bất phương trình \({\log _{\sqrt 2 }}(3 - 2x) > 1\)
Hướng dẫn làm bài
1) Đặt \({3^{{x \over {10}}}} = t(t > 0)\) , ta có:
\({t^2} + {t \over 3} = 84 \Leftrightarrow 3{t^2} + t - 252 = 0 \Leftrightarrow \left[ {\matrix{{t = 9} \cr {t = - 9{1 \over 3}(l)} \cr} } \right.\)
Như vậy \({3^{{x \over {10}}}} = {3^2} \Leftrightarrow x = 20\)
2) Điều kiện: \(3 - 2x > 0 \Leftrightarrow x < {3 \over 2}\)
Bất phương trình đã cho tương đương với \(3 - 2x > \sqrt 2 \)
\(\Leftrightarrow x < {{3 - \sqrt 2 } \over 2}\) (thỏa mãn điều kiện)
Câu 3 trang 225 sách bài tập (SBT) – Giải tích 12 (2,5 điểm)
1) Tính tích phân \(\int\limits_0^3 {{{\sqrt {x + 1} + 2} \over {\sqrt {x + 1} + 3}}} dx\) (đặt \(t = \sqrt {x + 1} \))
2) Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn điều kiện:
a) \(|z + 1| = |z - i|\) b) \(|z{|^2} + 3z + 3\overline z = 0\)
Hướng dẫn làm bài
1) Đặt \(t = \sqrt {x + 1} \Rightarrow {t^2} = x + 1\) . Do đó, \(dx = 2tdt\)
Khi x = 0 thì t = 1, khi x = 3 thì t = 2.
Vậy \(I = \int\limits_1^2 {{{(t + 2).2tdt} \over {t + 3}} = } \int\limits_1^2 {(2t - 2 + {6 \over {t + 3}})dt = 1 + 6\ln {5 \over 4}} \)
2) a) Giả sử \(z = x + yi\). Ta có: \(|x + 1 + yi| = |x + (y - 1)i|\)
\( \Leftrightarrow |(x + 1) + yi{|^2} = |x + (y - 1)i{|^2}\)
\( \Leftrightarrow {(x + 1)^2} + {y^2} = {x^2} + {(y - 1)^2}\)
\(\Leftrightarrow {x^2} + 1 + 2x + {y^2} = {x^2} + {y^2} + 1 - 2y\)
\(\Leftrightarrow 2x = -2y \,\,\,\,\,\, \Leftrightarrow y = -x\)
Trên mặt phẳng tọa độ, đó là đường phân giác của góc phần tư thứ hai và thứ tư.
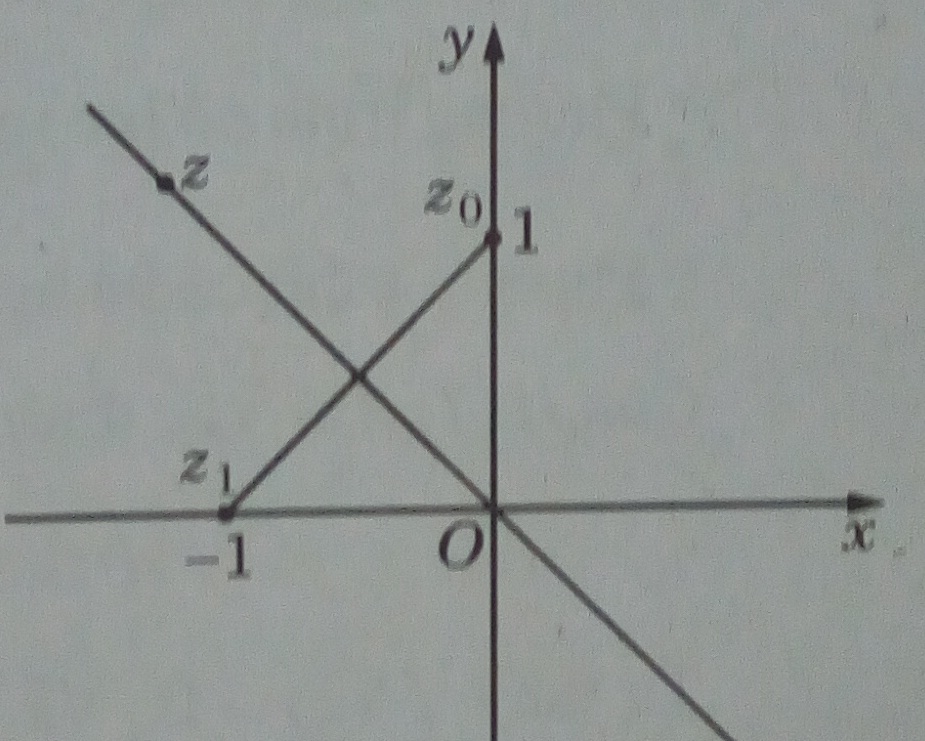
Cách 2. Vế phải là khoảng cách từ điểm biểu diễn z tới điểm biểu diễn \({z_0} = 0 + i\), vế trái là khoảng cách từ điểm biểu diễn z tới điểm biểu diễn \({z_1} = - 1 + 0i\) . Vậy phải tìm các điểm cách đều hai điểm biểu diễn z0 và z1
b) Ta có: \(|x + yi{|^2} + 3(x + yi) + 3(x - yi) = 0\)
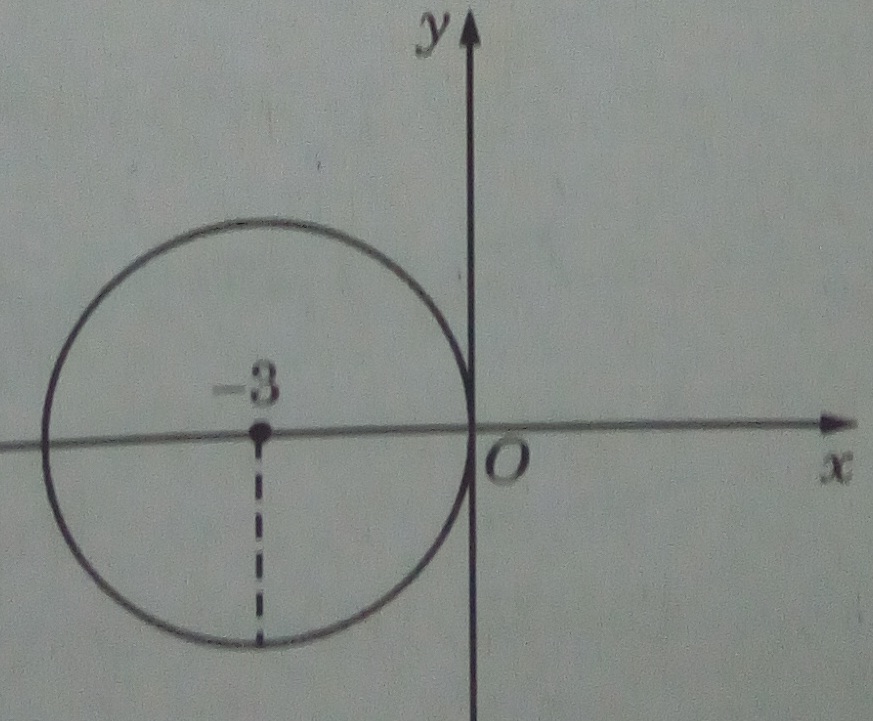
\(\Leftrightarrow {x^2} + {y^2} + 6x = 0 \Leftrightarrow {(x + 3)^2} + {y^2} = 9\)
Trên mặt phẳng tọa độ, đó là tập hợp các điểm thuộc đường tròn bán kính bằng 3 và tâm là điểm (-3; 0)
ĐỀ 3.
Câu 1 trang 225 sách bài tập (SBT) – Giải tích 12 (4 điểm)
Cho hàm số: \(y = - {x^3} + 3x - 2\)
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Viết phương trình tiếp tuyến của (C) tại điểm M(1; 0).
3) Biện luận theo m số nghiệm của phương trình \( - {x^3} + 3x - 2 = {\log _3}m\)
Hướng dẫn làm bài
1) Vẽ biểu đồ
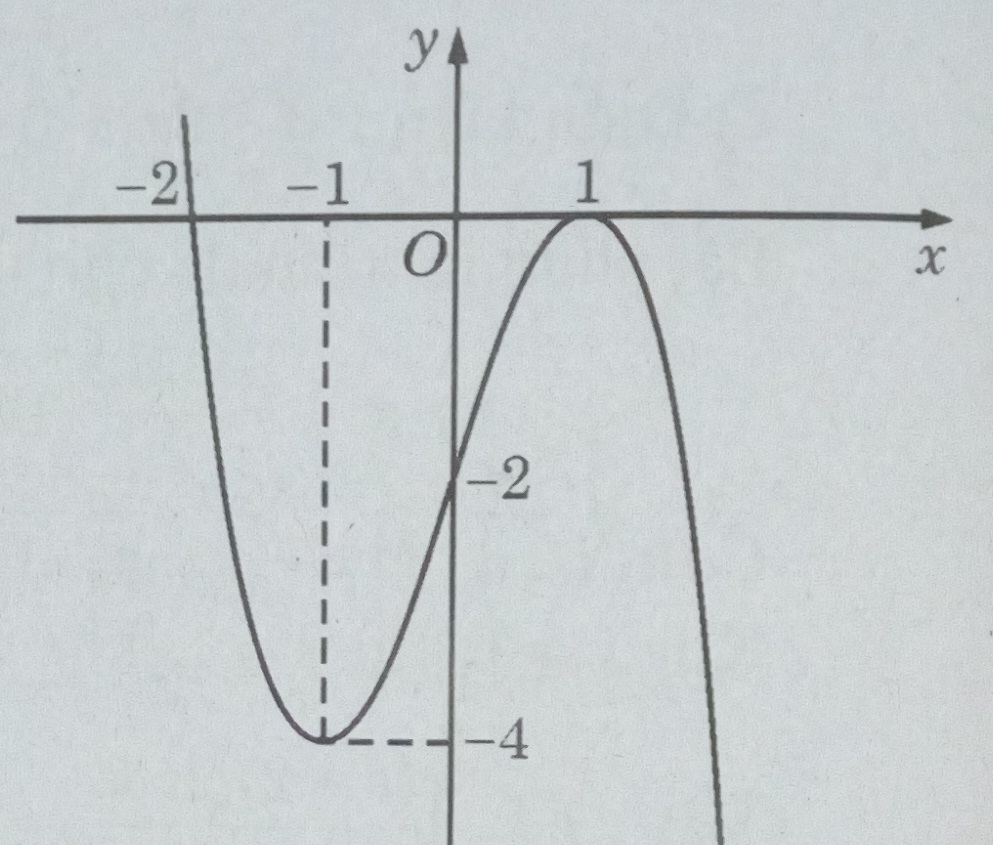
2) Ta có: y’(1) = 0. Vậy phương trình của tiếp tuyến là y = 0
3) Dựa vào đồ thị (C) và đường thẳng \(y = {\log _3}m\) , ta có:
* Khi \({\log _3}m < - 4 \Leftrightarrow m < {1 \over {81}}\), phương trình có một nghiệm
* Khi \({\log _3}m = - 4 \Leftrightarrow m = {1 \over {81}}\), phương trình có hai nghiệm.
* Khi \(0 > {\log _3}m > - 4 \Leftrightarrow 1 > m > {1 \over {81}}\), phương trình có ba nghiệm.
* Khi \({\log _3}m = 0 \Leftrightarrow m = 1\), phương trình có hai nghiệm.
* Khi \({\log _3}m > 0 \Leftrightarrow m > 1\) , phương trình có một nghiệm.
Kết luận:
* Phương trình có một nghiệm khi m > 1 hoặc \(m < {1 \over {81}}\)
* Phương trình có hai nghiệm khi m = 1 hoặc \(m = {1 \over {81}}\)
* Phương trình có ba nghiệm khi \({1 \over {81}} < m < 1\) .
Câu 2 trang 225 sách bài tập (SBT) – Giải tích 12 (3 điểm)
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
1) \(f(x) = \ln ({x^2} + x - 2)\) trên đoạn [3; 6]
2) \(f(x) = {\cos ^2}x + \cos x + 3\)
Hướng dẫn làm bài
1) f(x) xác định trên R\[-2; 1] nên xác định trên đoạn [3; 6]
\(f'(x) = {{2x + 1} \over {{x^2} + x - 2}}\)
Ta thấy \(f{\rm{ }}\left( x \right){\rm{ }} > {\rm{ }}0{\rm{ }},\forall x \in {\rm{[}}3;6]\) nên trên đoạn [3; 6] hàm số f(x) đồng biến.
Vậy \(\mathop {\min }\limits_{{\rm{[}}3;6]} f(x) = f(3) = \ln 10;\mathop {\max }\limits_{{\rm{[}}3;6]} f(x) = f(6) = \ln 40\)
2) Vì f(x) là hàm số tuần hoàn chu kì \(2\pi \), nên ta chỉ cần xét f(x) trên đoạn \({\rm{[}}0;2\pi {\rm{]}}\)
\(f'(x) = - 2\sin x\cos x - \sin x;f'(0) = 0 \Leftrightarrow x = {\rm{\{ }}0;{{2\pi } \over 3};\pi ;{{4\pi } \over 3};2\pi {\rm{\} }}\)
\(f(0) = f(2\pi ) = 5;f({{2\pi } \over 3}) = 2{3 \over 4};f(\pi ) = 3;f({{4\pi } \over 3}) = 2{3 \over 4}\)
Vậy \(\mathop {\min }\limits_R f(x) = \mathop {\min }\limits_{{\rm{[}}0;2\pi {\rm{]}}} f(x) = 2{3 \over 4};\mathop {\max }\limits_R f(x) = \mathop {\max }\limits_{{\rm{[}}0;2\pi {\rm{]}}} f(x) = 5\)
Câu 3 trang 226 sách bài tập (SBT) – Giải tích 12 (3 điểm)
1) Tính các tích phân sau:
a) \(\int\limits_0^1 {(3{x^2} + 2x + 1){e^{2x}}dx}\) b) \(\int\limits_0^{{\pi \over 2}} {\cos 3x} .\cos 4xdx\)
2) Tìm modun của các số phức sau:
a) \(z = ( - 4 + i\sqrt {48} )(2 + i)\) b) \(z = {{1 + i} \over {2 - i}}\)
Hướng dẫn làm bài
1) a) Đáp số : \({7 \over 4}{e^2} - {3 \over 4}\)
b) \(\int\limits_0^{{\pi \over 2}} {\cos 3x\cos 4xdx} = {1 \over 2}\int\limits_0^{{\pi \over 2}} {(\cos 7x + \cos x)dx = {3 \over 7}} \)
2) a) \(z = ( - 4 + i\sqrt {48} )(2 + i)\) nên
\(|z| = | - 4 + i\sqrt {48} |.|2 + i| = \sqrt {{{( - 4)}^2} + {{(\sqrt {48} )}^2}} .\sqrt {{2^2} + {1^2}} = 8\sqrt 5 \)
b) \(z = {{1 + i} \over {2 - i}}\) nên \(|z| = {{|1 + i|} \over {|2 - i|}} = {{\sqrt 2 } \over {\sqrt {{2^2} + {{( - 1)}^2}} }} = \sqrt {{2 \over 5}} \).
congdong.edu.vn