Lớp 12 - SBT Toán học Giải bài 1.35,1.36, 1.37 trang 23 Sách bài tập Giải tích 12
Bài 1.35 trang 22 sách bài tập (SBT) – Hình học 12
Cho tứ diện đều ABCD. Gọi (H) là hình bát diện đều có các đỉnh là trung điểm các cạnh của tứ diện đều đó. Tính tỉ số \({{{V_{(H)}}} \over {{V_{ABCD}}}}\).
Hướng dẫn làm bài
Gọi cạnh của tứ diện đều ABCD là a thì cạnh của hình bát diện đều (H) là \({a \over 2}\) . Khi đó \({V_{ABCD}} = {a^3}{{\sqrt 2 } \over {12}},{V_{(H)}} = {1 \over 3}{({a \over 2})^3}\sqrt 2 = {a^3}{{\sqrt 2 } \over {24}}\)
Từ đó suy ra \({{{V_{(H)}}} \over {{V_{ABCD}}}} = {1 \over 2}\).
Bài 1.36 trang 23 sách bài tập (SBT) – Hình học 12
Cho hình lập phương ABCD.A’B’C’D’ cạnh a, M là trung điểm của BB’ Tính theo a :
a) Khoảng cách giữa AC và DC’.
b) Độ dài đoạn vuông góc chung giữa CM và AB’.
Hướng dẫn làm bài
a)
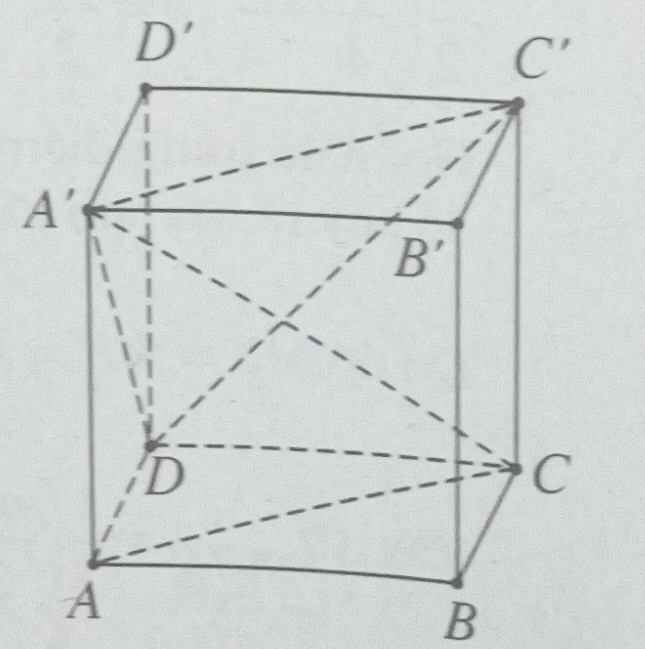
Gọi d(AC, DC’) = h
Ta có C’A’ // CA , do đó:
d(AC, DC’) = d(AC, (A’C’D)) = d(C, (A’C’D)) = h
Ta có: \({V_{A'.CDC'}} = {1 \over 3}{{{a^2}} \over 2}a = {{{a^3}} \over 6}\)
Để ý rằng tam giác A’C’D là tam giác đều cạnh bằng \(a\sqrt 2 \).
Do đó: \({S_{A'C'D}} = {{{a^2}\sqrt 3 } \over 2}\);
\({V_{C.A'C'D}} = {1 \over 3}{S_{A'C'D}}.h = {1 \over 3}.{{{a^2}\sqrt 3 } \over 2}h = {V_{A'.CDC'}} = {{{a^3}} \over 6}\)
Từ đó suy ra: \(h = {{{{{a^3}} \over 6}} \over {{{{a^2}\sqrt 3 } \over 6}}} = {a \over {\sqrt 3 }} = {{a\sqrt 3 } \over 3}\)
b)
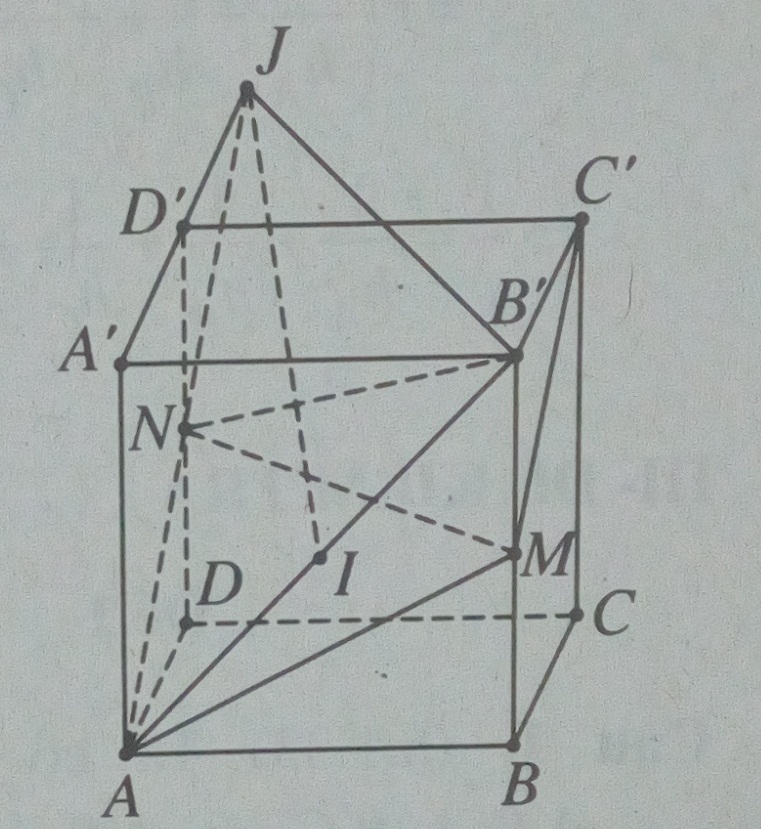
Từ A kẻ đường thẳng song song với MC’ , cắt DD’ tại N và A’D’ kéo dài tại J.
Đặt h1 = d(MC’ , AB’) = d(M, (AB’N))
Ta có: \({V_{M.AB'N}} = {V_{N.AB'M}} = {1 \over 3}{{{a^2}} \over 4}a = {{{a^3}} \over {12}}\)
Để ý rằng N là trung điểm của DD’ , A’J = 2A’D’ và JA = JB’
Gọi I là trung điểm của AB’, khi đó \(JI \bot AB'\).
Ta có: \({\rm{AJ}} = \sqrt {{\rm{AA}}{'^2} + A'{J^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 ;AI = {{a\sqrt 2 } \over 2}\)
Suy ra: \({\rm{IJ}} = \sqrt {5{a^2} - {{{a^2}} \over 2}} = {{3a} \over {\sqrt 2 }}\) ;
\({S_{JAB'}} = {1 \over 2}{{3a} \over {\sqrt 2 }}a\sqrt 2 = {{3{a^2}} \over 2}\)
Do đó: \({S_{AB'N}} = {1 \over 2}{S_{JAB'}} = {{3{a^2}} \over 4}\) ;
\({V_{M.AB'N}} = {1 \over 3}{{3{a^2}} \over 4}{h_1} = {{{a^2}{h_1}} \over 4} = {{{a^3}} \over {12}}\)
Suy ra: \({h_1} = {a \over 3}\)
Chú ý: Có thể tính thể tích SAB’N bằng cách khác.
Để ý rằng: \(NB' = \sqrt {ND{'^2} + B'D{'^2}} = \sqrt {{{{a^2}} \over 4} + 2{a^2}} = {{3a} \over 2},\)
\(AN = {{a\sqrt 5 } \over 2},\,\,AB' = a\sqrt 2 \)
Gọi \(\alpha = \widehat {NAB'}\) . Ta có: \(NB{^2} = {\rm{ }}A{N^2} + {\rm{ }}AB{^2}-{\rm{ }}2AN.AB.cos\alpha \)
Hay \({{9{a^2}} \over 4} = {{5{a^2}} \over 4} + 2{a^2} - 2{{a\sqrt 5 } \over 2}a\sqrt 2 \cos \alpha\)
\( \Rightarrow \cos \alpha = {1 \over {\sqrt {10} }} \Rightarrow \sin \alpha = {3 \over {\sqrt {10} }}\)
Do đó: \({S_{AB'N}} = {1 \over 2}AB'.AN.\sin \alpha = {1 \over 2}a\sqrt 2 {{a\sqrt 5 } \over 2}{3 \over {\sqrt {10} }} = {{3{a^2}} \over 4}\)
Bài 1.37 trang 23 sách bài tập (SBT) – Hình học 12
Cho tứ diện ABCD. Gọi hA , hB, hC, hD lần lượt là các đường cao của tứ diện xuất phát từ A, B, C, D và r là bán kính mặt cầu nội tiếp tứ diện. Chứng minh rằng:
\({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}} = {1 \over r}\)
Hướng dẫn làm bài:
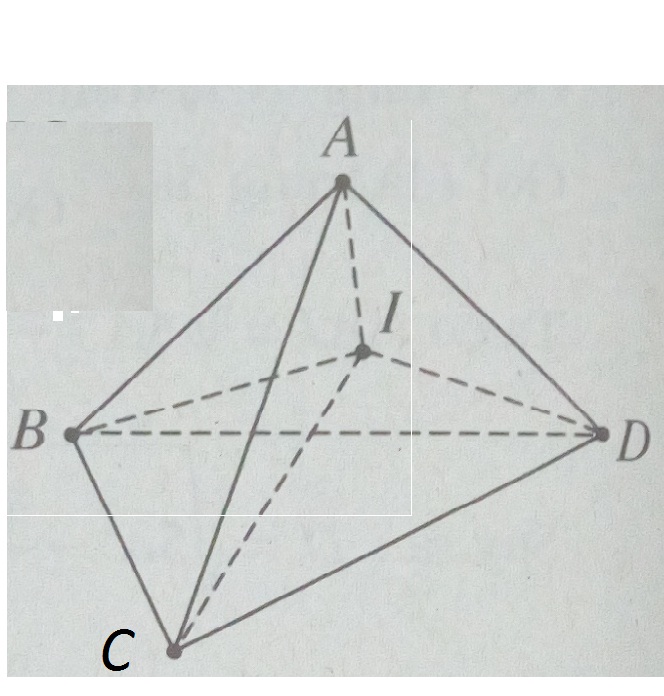
Gọi I là tâm mặt cầu nội tiếp tứ diện, V là thể tích tứ diện. Ta có
\(V = {V_{IBCD}} + {V_{ICDA}} + {V_{IDAB}} + {V_{IABC}}\)
\( \Rightarrow I = {{{V_{IBCD}}} \over V} + {{{V_{ICDA}}} \over V} + {{{V_{IDAB}}} \over V} + {{{V_{IABC}}} \over V}\)
\(= {{{1 \over 3}r{S_{BCD}}} \over {{1 \over 3}{h_A}{S_{BCD}}}} + {{{1 \over 3}r{S_{CDA}}} \over {{1 \over 3}{h_B}{S_{CDA}}}} + {{{1 \over 3}r{S_{DAB}}} \over {{1 \over 3}{h_C}{S_{DAB}}}} + {{{1 \over 3}r{S_{ABC}}} \over {{1 \over 3}{h_D}{S_{ABC}}}}\)
\( = r({1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}})\)
\(\Rightarrow {1 \over r} = {1 \over {{h_A}}} + {1 \over {{h_B}}} + {1 \over {{h_C}}} + {1 \over {{h_D}}}\)
congdong.edu.vn