Lớp 12 - SBT Toán học Giải bài 2.39, 2.40, 2.41, 2.42 trang 131, 132 Sách bài tập (SBT) Giải tích 12
Bài 2.39 trang 131, 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình mũ sau:
a) \({3^{|x - 2|}} < 9\)
b) \({4^{|x + 1|}} > 16\)
c) \({2^{ - {x^2} + 3x}} < 4\)
d) \({(\frac{7}{9})^{2{x^2} - 3x}} \ge \frac{9}{7}\)
e) \({11^{\sqrt {x + 6} }} \ge {11^x}\)
g) \({2^{2x - 1}} + {2^{2x - 2}} + {2^{2x - 3}} \ge 448\)
h)\({16^x} - {4^x} - 6 \le 0\)
i) \(\frac{{{3^x}}}{{{3^x} - 2}} < 3\)
Hướng dẫn làm bài:
a) \({3^{|x - 2|}} < {3^2}\)
\( \Leftrightarrow |x - 2| < 2\)
\( \Leftrightarrow - 2 < x - 2 < 2\)
\( \Leftrightarrow 0 < x < 4\)
b)
\({4^{|x + 1|}} > {4^2}\)
\( \Leftrightarrow |x + 1| > 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x + 1 > 2}\\
{x + 1 < - 2}
\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x > 1}\\
{x < - 3}
\end{array}} \right.\)
c)
\({2^{ - {x^2} + 3x}} < {2^2}\)
\( \Leftrightarrow - {x^2} + 3x < 2 \)
\( \Leftrightarrow {x^2} - 3x + 2 > 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x < 1}\\
{x > 2}
\end{array}} \right.\)
d)
\({(\frac{7}{9})^{2{x^2} - 3x}} \ge {(\frac{7}{9})^{ - 1}}\)
\( \Leftrightarrow 2{x^2} - 3x \le - 1\)
\( \Leftrightarrow 2{x^2} - 3x + 1 \le 0 \Leftrightarrow \frac{1}{2} \le x \le 1\)
e)
\(\eqalign{& \sqrt {x + 6} \ge x \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x + 6 \ge 0} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {x + 6 \ge {x^2}} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{\left\{ {\matrix{{x \ge - 6} \cr {x < 0} \cr} } \right.} \cr {\left\{ {\matrix{{x \ge 0} \cr {{x^2} - x - 6 \le 0} \cr} } \right.} \cr} } \right. \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {\left\{ {\matrix{{ - 2 \le x \le 3} \cr {x \ge 0} \cr} } \right.} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{ - 6 \le x < 0} \cr {0 \le x \le 3} \cr} } \right. \Leftrightarrow - 6 \le x \le 3 \cr}\)
g)
\(\frac{1}{2}{.2^{2x}} + \frac{1}{4}{.2^{2x}} + \frac{1}{8}{.2^{2x}} \ge 448\)
\( \Leftrightarrow {2^{2x}} \ge 512 \Leftrightarrow {2^{2x}} \ge {2^9} \Leftrightarrow x \ge \frac{9}{2}\)
h) Đặt t = 4x (t > 0), ta có hệ bất phương trình:
\(\eqalign{& \left\{ {\matrix{{{t^2} - t - 6 \le 0} \cr {t > 0} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{ - 2 \le t \le 3} \cr {t > 0} \cr} } \right. \cr & \Leftrightarrow 0 < t \le 3 \Leftrightarrow 0 < {4^x} \le 3 \Leftrightarrow x \le {\log _4}3 \cr} \)
i)
\(\eqalign{& {{{3^x}} \over {{3^x} - 2}} - 3 < 0 \Leftrightarrow {{ - {{2.3}^x} + 6} \over {{3^x} - 2}} < 0 \cr & \Leftrightarrow {{{3^x} - 3} \over {{3^x} - 2}} > 0 \Leftrightarrow \left[ {\matrix{{{3^x} > 3} \cr {{3^x} < 2} \cr} } \right. \Leftrightarrow \left[ {\matrix{{x > 1} \cr {x < {{\log }_3}2} \cr} } \right. \cr} \)
Bài 2.40 trang 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình logarit sau:
a) \({\log _{\frac{1}{3}}}(x - 1) \ge - 2\)
b) \({\log _3}(x - 3) + {\log _3}(x - 5) < 1\)
c) \({\log _{\frac{1}{2}}}\frac{{2{x^2} + 3}}{{x - 7}} < 0\)
d) \({\log _{\frac{1}{3}}}{\log _2}{x^2} > 0\)
e) \(\frac{1}{{5 - \log x}} + \frac{2}{{1 + \log x}} < 1\)
g) \(4{\log _4}x - 33{\log _x}4 \le 1\)
Hướng dẫn làm bài:
a) \(0 < x - 1 \le {(\frac{1}{3})^{ - 2}} \Leftrightarrow 1 < x \le 10\)
b)
\(\eqalign{& \left\{ {\matrix{{x > 5} \cr {{{\log }_3}{\rm{[}}(x - 3)(x - 5){\rm{]}} < {{\log }_3}3} \cr} } \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {{x^2} - 8x + 12 < 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 5} \cr {2 < x < 6} \cr} } \right.} \right. \cr & \Leftrightarrow 5 < x < 6 \cr} \)
c)
\(\eqalign{& \left\{ {\matrix{{x - 7 > 0} \cr {{{2{x^2} + 3} \over {x - 7}} > 1} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} + 3 > x - 7} \cr} } \right.} \right. \cr & \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {2{x^2} - x + 10 > 0} \cr} \Leftrightarrow \left\{ {\matrix{{x > 7} \cr {x \in R} \cr} \Leftrightarrow x > 7} \right.} \right. \cr} \)
d)
\(\eqalign{
& {\log _{{1 \over 3}}}{\log _2}{x^2} > {\log _{{1 \over 3}}}1 \cr
& \Leftrightarrow {\log _2}{x^2} < 1 \cr
& \Leftrightarrow {\log _2}{x^2} < {\log _2}2 \cr
& \Leftrightarrow 0 < {x^2} < 2 \cr} \)
\(\Leftrightarrow 0 < |x| < \sqrt 2 \Leftrightarrow \left[ {\matrix{{ - \sqrt 2 < x < 0} \cr {0 < x < \sqrt 2 } \cr} } \right.\)
e) Đặt \(t = \log x\) với điều kiện \(t \ne 5,t \ne - 1\) ta có:
\(\eqalign{
& {1 \over {5 - t}} + {2 \over {1 + t}} < 1 \Leftrightarrow {{t + 1 + 10 - 2t} \over {5 + 4t - {t^2}}} - 1 < 0 \cr
& \Leftrightarrow {{{t^2} - 5t + 6} \over {{t^2} - 4t - 5}} > 0 \Leftrightarrow {{(t - 2)(t - 3)} \over {(t + 1)(t - 5)}} > 0 \cr & \Leftrightarrow \left[ {\matrix{{t < - 1} \cr {2 < t < 3} \cr {t > 5} \cr} } \right. \cr} \)
Suy ra log x < -1 hoặc 2 < log x < 3 hoặc log x > 5.
Vậy \(x < \frac{1}{{10}}\) hoặc 100 < x < 1000 hoặc x > 100 000.
g) Với điều kiện \(x > 0,x \ne 1\) đặt \(t = {\log _4}x\) , ta có: \(4t - \frac{{33}}{t} \le 1\)
\(\eqalign{& \Leftrightarrow {{4{t^2} - t - 33} \over t} \le 0 \Leftrightarrow {{(4t + 11)(t - 3)} \over t} \le 0 \cr & \Leftrightarrow \left[ {\matrix{{t \le - {{11} \over 4}} \cr {0 < t \le 3} \cr} } \right. \cr & \Leftrightarrow \left[ {\matrix{{{{\log }_4}x \le - {{11} \over 4}} \cr {0 < {{\log }_4}x \le 3} \cr} } \right. \Leftrightarrow \left[ {\matrix{{0 < x \le {4^{ - {{11} \over 4}}}} \cr {1 < x \le 64} \cr} } \right. \cr} \)
Bài 2.41 trang 132 Sách bài tập (SBT) Giải tích 12
Giải các bất phương trình sau bằng đồ thị:
a) \({(\frac{1}{2})^x} < x - \frac{1}{2}\)
b) \({(\frac{1}{3})^x} \ge x + 1\)
c) \({\log _{\frac{1}{3}}}x > 3x\)
d) \({\log _2}x \le 6 - x\)
Hướng dẫn làm bài:
a) Vẽ đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) và đường thẳng \(y = x - \frac{1}{2}\) trên cùng một hệ trục tọa độ (H.65), ta thấy chúng cắt nhau tại điểm có hoành độ x = 1. Với x > 1 đồ thị của hàm số \(y = {(\frac{1}{2})^x}\) nằm phía dưới đường thẳng \(y = x - \frac{1}{2}\) . Vậy tập nghiệm của bất phương trình đã cho là \((1; + \infty )\)
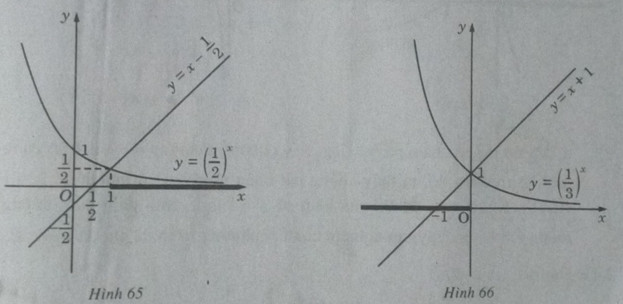
b) Vẽ đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) và đường thẳng y = x + 1 trên cùng một hệ trục tọa độ (H.66), ta thấy chúng cắt nhau tại điểm có hoành độ x = 0.
Khi x < 0 đồ thị của hàm số \(y = {(\frac{1}{3})^x}\) nằm phía trên đường thẳng y = x + 1. Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;0]\)
c) Vẽ đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) và đường thẳng y = 3x trên cùng một hệ trục tọa độ ta thấy chúng cắt nhau tại điểm có hoành độ \(x = \frac{1}{3}\) (H.67)
Khi \(x < \frac{1}{3}\) đồ thị của hàm số \(y = {\log _{\frac{1}{3}}}x\) nằm phía trên đường thẳng y = 3x.
Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;\frac{1}{3})\) .
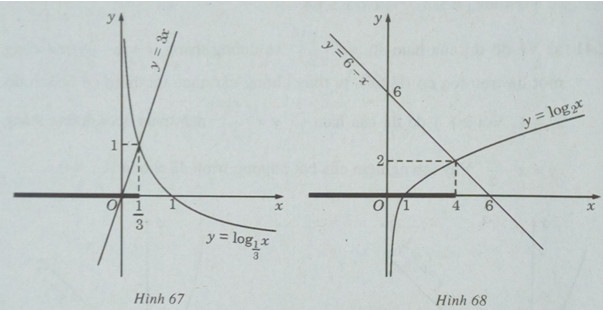
d) Vẽ đồ thị của hàm số \(y = {\log _2}x\) và đường thẳng y = 6 – x trên cùng một hệ trục tọa độ, ta thấy chúng cắt nhau tại điểm có hoành độ x = 4 (H.68).
Khi x < 4, đồ thị của hàm số \(y = {\log _2}x\) nằm phía dưới y = 6 – x .
Vậy tập nghiệm của bất phương trình đã cho là \(( - \infty ;4]\).
Bài 2.42 trang 132 Sách bài tập (SBT) Giải tích 12
Giải bất phương trình : \({\log _{\frac{1}{3}}}({\log _2}\frac{{2x + 3}}{{x + 1}}) \ge 0\)
Trả lời:
Đáp số : x < - 2.
congdong.edu.vn