Lớp 12 - SBT Toán học Giải bài 1.17, 1.18, 1.19 trang 16 Sách bài tập Giải tích 12
Bài 1.17 trang 16 Sách bài tập (SBT) Giải tích 12
Xác định m để hàm số: \(y = {x^3} - m{x^2} + (m - {2 \over 3})x + 5\) có cực trị tại x = 1. Khi đó, hàm số đạt cực tiểu hay đạt cực đại? Tính cực trị tương ứng.
Hướng dẫn làm bài:
\(y = {x^3} - m{x^2} + (m - {2 \over 3})x + 5\)
Ta biết hàm số y = f(x) có cực trị khi phương trình y’ = 0 có nghiệm và y’ đổi dấu khi qua các nghiệm đó.
Ta có:
Xét y’ = 0, ta có: \(y' = 3{x^2} - 2mx + (m - {2 \over 3})\)
∆’ > 0 khi m < 1 hoặc m > 2 (*)
Để hàm số có cực trị tại x = 1 thì
\(y'(1) = 3 - 2m + m - {2 \over 3} = 0 < = > m = {7 \over 3}\) , thỏa mãn điều kiện (*)
Với \(m = {7 \over 3}\) thì hàm số đã cho trở thành:
\(y = {x^3} - {7 \over 3}{x^2} + {5 \over 3}x + 5\)
Ta có:
\(\eqalign{
& y' = 3{x^2} - {{14} \over 3}x + {5 \over 3} \cr
& y'' = 6x - {{14} \over 3} \cr} \)
Vì \(y''(1) = 6 - {{14} \over 3} > 0\) nên hàm số đạt cực tiểu tại x = 1 và \({y_{CT}} = {y_{\left( 1 \right)}} = {{16} \over 3}.\)
Bài 1.18 trang 16 Sách bài tập (SBT) Giải tích 12
Chứng minh rằng hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Không có đạo hàm tại x = 0 nhưng đạt cực đại tại điểm đó.
Hướng dẫn làm bài:
Hàm số:
\(f(x) = \left\{ \matrix{
- 2x,\forall x \ge 0 \hfill \cr
\sin {x \over 2},\forall x < 0 \hfill \cr} \right.\)
Không có đạo hàm tại x = 0 vì:
\(\eqalign{
& \mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2 \cr
& \mathop {\lim }\limits_{x \to {0^ + }} {{f(x) - f(0)} \over x} = \mathop {\lim }\limits_{x \to {0^ + }} {{ - 2x} \over x} = - 2 \cr} \)
Mặt khác, với x < 0 thì \(y' = {1 \over 2}\cos {x \over 2}\) , với x > 0 thì y’ = -2 < 0
Bảng biến thiên:
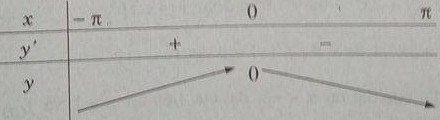
Từ đó ta thấy hàm số đạt cực đại tại x = 0 và yCĐ = y(0) = 0.
Bài 1.19 trang 16 Sách bài tập (SBT) Giải tích 12
Xác định giá trị m để hàm số sau không có cực trị.
\(y = {{{x^2} + 2mx - 3} \over {x - m}}\)
Hướng dẫn làm bài:
Hàm số không có cực trị khi đạo hàm của nó không đổi dấu trên tập xác định \(D=\mathbb R\backslash {\rm{\{ }}m{\rm{\} }}\)
Ta có:
\(\eqalign{
& y = {{{x^2} + 2mx - 3} \over {x - m}} \cr
& y' = {{(2x + 2m)(x - m) - ({x^2} + 2mx - 3)} \over {{{(x - m)}^2}}} \cr
& = {{2{x^2} - 2{m^2} - {x^2} - 2mx + 3} \over {{{(x - m)}^2}}} = {{{x^2} - 2mx - 2{m^2} + 3} \over {{{(x - m)}^2}}} \cr} \)
Xét g(x) = x2 – 2mx – 2m2 + 3
∆’g = m2 + 2m2 – 3 = 3(m2 – 1) ;
∆’g ≤ 0 khi – 1 ≤ m ≤ 1.
Khi – 1 ≤ m ≤ 1 thì phương trình g(x) = 0 vô nghiệm hay y’ = 0 vô nghiệm và y’ > 0 trên tập xác định. Khi đó, hàm số không có cực trị.
Khi m = 1 hoặc m = -1, hàm số đã cho trở thành y = x + 3 (với x ≠ 1) hoặc y = x – 3 (với x ≠ - 1) Các hàm số này không có cực trị.
Vậy hàm số đã cho không có cực trị khi – 1 ≤ m ≤ 1.
congdong.edu.vn