Lớp 12 - SBT Toán học Giải bài 1.8, 1.9, 1.10 trang 8,9 Sách bài tập Giải tích 12

Bài 1.8 trang 8 Sách bài tập (SBT) Giải tích 12

Chứng minh các bất đẳng thức sau:

a) \(\tan x > \sin x,0 < x < {\pi \over 2}\)

b) \(1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x} < 1 + {1 \over 2}x\) với \(0 < x < + \infty \)

Hướng dẫn làm bài:

a) Xét hàm số \(f(x) = \tan x - \sin x\) trên nửa khoảng \({\rm{[}}0;{\pi \over 2})\) ;

\(f'(x) = {1 \over {{{\cos }^2}x}} - \cos x = {{1 - {{\cos }^3}x} \over {{{\cos }^2}}} \ge 0;x \in {\rm{[}}0;{1 \over 2})\)

Dấu “=” xảy ra khi x = 0.

Suy ra f(x) đồng biến trên nửa khoảng \({\rm{[}}0;{\pi \over 2})\)

Mặt khác, ta có f(0) = 0, nên f(x) = tan x – sin x > 0 hay tan x > sin x với mọi \(x \in {\rm{[}}0;{1 \over 2})\)

b) Xét hàm số \(h(x) = 1 + {1 \over 2}x - \sqrt {1 + x}\) trên $${\rm{[}}0; + \infty )$$

\(\eqalign{
& h'(x) = {1 \over 2} - {1 \over {2\sqrt {1 + x} }} \ge 0 \cr
& 1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x} ,0 \le x \le + \infty \cr} \)

Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng \({\rm{[}}0; + \infty )\).

Vì h(x) = 0 nên \(h(x) = 1 + {1 \over 2}x - \sqrt {1 + x} > 0\)

Hay \(1 + {1 \over 2}x > \sqrt {1 + x} \) với \(0 \le x < + \infty \)

Xét hàm số trên \(f(x) = \sqrt {1 + x} - 1 - {1 \over 2}x + {{{x^2}} \over 8}\) trên \({\rm{[}}0; + \infty )\) ;

\(\eqalign{
& g(x) = f'(x) = {1 \over {2\sqrt {1 + x} }} - {1 \over 2} + {x \over 4} \cr
& g'(x) = {1 \over 4} - {1 \over {4(1 + x)\sqrt {1 + x} }} \ge 0,0 \le x < + \infty \cr} \)

Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng \({\rm{[}}0; + \infty )\) nên \(g(x) \ge 0\) , tức là \(f'(x) \ge 0\) trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .

Mặt khác, ta có f(0) = 0 nên

\(f(x) = \sqrt {1 + x} - 1 - {1 \over 2}x + {{{x^2}} \over 8} > 0\)

hay \(1 + {1 \over 2}x - {{{x^2}} \over 8} < \sqrt {1 + x} \)

Với mọi \(0 < x < + \infty \).

Bài 1.9 trang 9 Sách bài tập (SBT) Giải tích 12

Chứng minh rằng phương trình \({x^3} - 3x + c = 0\) không thể có hai nghiệm thực trong đoạn [0; 1].

Hướng dẫn làm bài:

Đặt \(f(x) = {x^3} - 3x + C\) . TXĐ: R

\(f'(x) = 3{x^2} - 3 = 3({x^2} - 1)\)

\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 1 \hfill \cr} \right.\)

Bảng biến thiên:

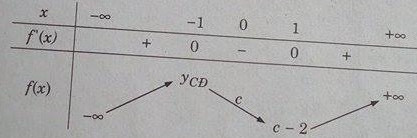
Trên đoạn [0; 1] hàm số f(x) nghịch biến nên đồ thị của hàm số f(x) không thể cắt trục hoành tại hai điểm trên đoạn này, tứclà phương trình x³ – 3x + C = 0 không thể có hai nghiệm thực trên đoạn [0; 1].

Bài 1.10 trang 9 Sách bài tập (SBT) Giải tích 12

Xác định giá trị của b để hàm số f(x) = \(\sin x - bx + c\) nghịch biến trên toàn trục số.

Hướng dẫn làm bài:

\(f(x) = \sin x - bx + c\) nghịch biến trên R nếu ta có:

\(f'(x) = \cos x - b \le 0,\forall x \in R\) .

Vì \(|\cos x| \le 1\) nên \(f'(x) \le 0,\forall x \in R < = > b \ge 1.\)

                                                                                                         congdong.edu.vn