Lớp 12 - SBT Toán học Giải bài 1.20, 1.21, 1.22 trang 19 Sách bài tập Giải tích 12
Bài 1.20 trang 19 Sách bài tập (SBT) Giải tích 12
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = -3x2 + 4x – 8 trên đoạn [0; 1]
b) f(x) = x3 + 3x2 – 9x – 7 trên đoạn [-4; 3]
c) \(f(x) = \sqrt {25 - {x^2}} \) trên đoạn [-4; 4]
d) f(x) = |x2 – 3x + 2| trên đoạn [-10; 10]
e) \(f(x) = {1 \over {\sin x}}\) trên đoạn \({\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}\)
g) \(f(x) = 2\sin x + \sin 2x\) trên đoạn \({\rm{[}}0;{{3\pi } \over 2}{\rm{]}}\)
Hướng dẫn làm bài:
a) f(x) = -3x2 + 4x – 8 trên đoạn [0; 1]
\(\eqalign{
& f'(x) = - 6x + 4,f'(x) = 0 < = > x = {2 \over 3} \cr
& f({2 \over 3}) = - {{20} \over 3},f(0) = - 8;f(1) = - 7 \cr} \)
Vậy \(\mathop {\min }\limits_{{\rm{[}}0;1]} f(x) = - 8;\mathop {\max }\limits_{{\rm{[}}0;1]} f(x) = - {{20} \over 3}\)
b) f(x) = x3 + 3x2 – 9x – 7 trên đoạn [-4; 3]
\(f'(x) = 3{x^2} + 6x - 9\)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
x = 1 \hfill \cr
x = - 3 \hfill \cr} \right.\)
Hàm số đạt cực đại tại x = -3, đạt cực tiểu tại x = 1 và fCĐ = f(-3) = 20; fCT = f(1) = -12 ;
f(-4) = 13 ; f(3) = 20.
Vậy \(\mathop {\min }\limits_{{\rm{[}} - 4;3]} f(x) = - 12;\mathop {\max }\limits_{{\rm{[}} - 4;3]} f(x) = 20\)
c) \(f(x) = \sqrt {25 - {x^2}} \) trên đoạn [-4; 4]
\(f'(x) = {{ - x} \over {\sqrt {25 - {x^2}} }};f'(x) > 0\) trên khoảng (-4; 0) và
f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và fCĐ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy \(\mathop {\min }\limits_{{\rm{[}} - 4;4]} f(x) = 3;\mathop {\max }\limits_{{\rm{[}} - 4;4]} f(x) = 5\)
d) \(f(x) = |{x^2} - 3x + 2|\) trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x2 – 3x + 2.
Ta có:
\(g'(x) = 2x - 3;g'(x) = 0 < = > x = {3 \over 2}\)
Bảng biến thiên:
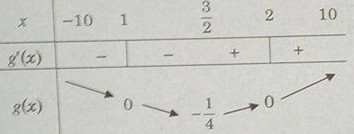
Vì
\(f(x) = \left\{ \matrix{
g(x),{x^2} - 3x + 2 \ge 0 \hfill \cr
- g(x),{x^2} - 3x + 2 < 0 \hfill \cr} \right.\)
nên ta có đồ thị f(x) như sau:
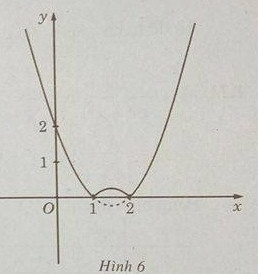
Từ đồ thị suy ra: \(\mathop {\min }\limits_{{\rm{[}} - 10;10]} f(x) = f(1) = f(2) = 0;\mathop {\max }\limits_{{\rm{[}} - 10;10]} f(x) = f( - 10) = 132\)
e) \(f(x) = {1 \over {\sin x}}\) trên đoạn \({\rm{[}}{\pi \over 3};{{5\pi } \over 6}{\rm{]}}\)
\(f'(x) = - {{\cos x} \over {{{\sin }^2}x}},f'(x) < 0\) nên và f’(x) > 0 trên \(({\pi \over 2};{{5\pi } \over 6}{\rm{]}}\) nên hàm số đạt cực tiểu tại \(x = {\pi \over 2}\) và \({f_{CT}} = f({\pi \over 2}) = 1\)
Mặt khác, \(f({\pi \over 3}) = {2 \over {\sqrt 3 }},f({{5\pi } \over 6}) = 2\)
Vậy \(\mathop {\min }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 1;\mathop {\max }\limits_{{\rm{[}}{\pi \over 3};{{5\pi } \over 6}]} f(x) = 2\)
g) \(f(x) = 2\sin x + \sin 2x\) trên đoạn \({\rm{[}}0;{{3\pi } \over 2}{\rm{]}}\)
\(f'(x) = 2\cos x + 2\cos 2x = 4\cos {x \over 2}\cos {{3x} \over 2}\)
\(f'(x) = 0 \Leftrightarrow \left[ \matrix{
\cos {x \over 2} = 0 \hfill \cr
\cos {{3x} \over 2} = 0 \hfill \cr} \right. \Rightarrow \left[ \matrix{
x = \pi \hfill \cr
x = {\pi \over 3} \hfill \cr} \right.\)
Ta có: \(f(0) = 0,f({\pi \over 3}) = {{3\sqrt 3 } \over 2},f(\pi ) = 0,f({{3\pi } \over 2}) = - 2\)
Từ đó ta có : \(\mathop {\min }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = - 2;\mathop {\max }\limits_{{\rm{[}}0;{{3\pi } \over 2}]} f(x) = {{3\sqrt 3 } \over 2}\).
Bài 1.21 trang 20 Sách bài tập (SBT) Giải tích 12
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\) .
Hướng dẫn làm bài:
a) \(y = {x \over {4 + {x^2}}}\) trên khoảng \(( - \infty ; + \infty )\)
\(\eqalign{
& y' = {{4 - {x^2}} \over {{{(4 + {x^2})}^2}}} \cr
& y' = 0 \Rightarrow \left[ \matrix{
x = - 2 \hfill \cr
x = 2 \hfill \cr} \right. \cr} \)
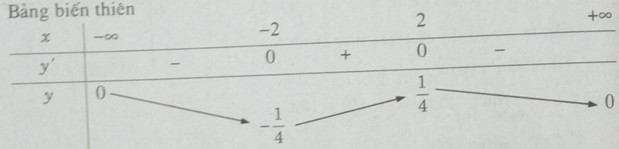
Từ đó ta có \(\mathop {\min }\limits_R f(x) = - {1 \over 4};\mathop {\max }\limits_R f(x) = {1 \over 4}\)
b) \(y = {1 \over {\cos x}}\) trên khoảng \(({\pi \over 2};{{3\pi } \over 2})\)
\(y' = {{\sin x} \over {{{\cos }^2}x}};y' = 0 < = > x = \pi\)
Bảng biến thiên:
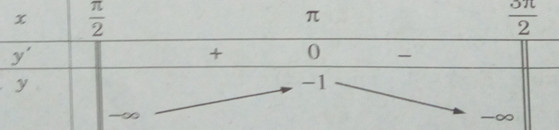
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất của hàm số là: \(\mathop {\max }\limits_{({\pi \over 2};{{3\pi } \over 2})} y = y(\pi ) = - 1\)
c) \(y = {1 \over {1 + {x^4}}}\) trên khoảng \(( - \infty ; + \infty )\) ;
\(y' = {{ - 4{x^3}} \over {{{(1 + {x^4})}^2}}};y' = 0 < = > x = 0\)
Bảng biến thiên:
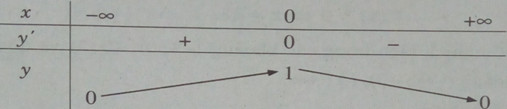
Hàm số không có giá trị nhỏ nhất. Giá trị lớn nhất là: \(\mathop {\max }\limits_R y = y(0) = 1\)
d) \(y = {1 \over {\sin x}}\) trên khoảng \((0;\pi )\)
\(y' = {{ - \cos x} \over {{{\sin }^2}x}},y' = 0 < = > x = {\pi \over 2}\)
Bảng biến thiên:
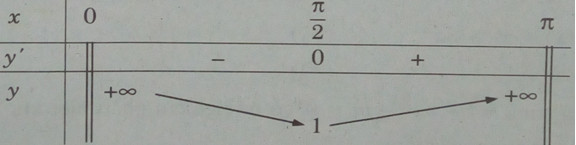
Hàm số không có giá trị lớn nhất. Giá trị nhỏ nhất của hàm số là: \(\mathop {\min }\limits_{(0;\pi )} y = y({\pi \over 2}) = 1\).
Bài 1.22 trang 20 Sách bài tập (SBT) Giải tích 12
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f(x) = {{2x - 1} \over {x - 3}}\) trên đoạn [0; 2].
(Đề thi tốt nghiệp THPT năm 2008, lần 2)
Hướng dẫn làm bài:
TXĐ: D =R\{3}
\(f'(x) = - {5 \over {{{(x - 3)}^2}}} < 0,\forall x \in D\) và do đó f(x) nghịch biến trên các khoảng \(( - \infty ;3),(3; + \infty )\)
Ta thấy \({\rm{[}}0;2] \subset ( - \infty ;3).\)
Vì vậy: \(\mathop {\min }\limits_{{\rm{[}}0;2]} f(x) = f(2) = - 3;\mathop {\max }\limits_{{\rm{[}}0;2]} f(x) = f(0) = {1 \over 3}\).
congdong.edu.vn