Lớp 12 - SBT Toán học Giải bài 3.9, 3.10, 3.11, 3.12 trang 103 Sách bài tập Hình học 12
Bài 3.9 trang 103 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz cho một vecto \(\overrightarrow a \) tùy ý khác vecto \(\overrightarrow 0 \). Gọi \(\alpha ,\beta ,\gamma \) là ba góc tạo bởi ba vecto đơn vị \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \) trên ba trục Ox, Oy, Oz và vecto \(\overrightarrow a \) . Chứng minh rằng: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
Hướng dẫn làm bài:
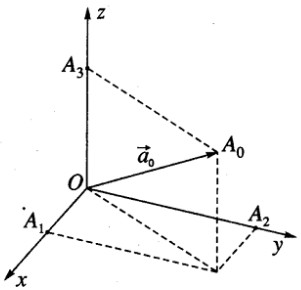
Gọi \(\overrightarrow {{a_0}} \) là vecto đơn vị cùng hướng với vecto \(\overrightarrow a \) , ta có \(\overrightarrow {{a_0}} = {1 \over {|\overrightarrow a |}}\overrightarrow a \).
Gọi \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) và các điểm A1, A2, A3 theo thứ tự là hình chiếu vuông góc của điểm A0 trên các trục Ox, Oy, Oz.
Khi đó ta có: \({{|\overrightarrow {O{A_1}} |} \over {|\overrightarrow {O{A_0}} |}} = \cos \alpha ,{{|\overrightarrow {O{A_2}} |} \over {|\overrightarrow {O{A_0}|} }} = \cos \beta ,{{|\overrightarrow {O{A_3}} |} \over {|\overrightarrow {O{A_0}} |}} = \cos \gamma \)
Vì \(|\overrightarrow {O{A_0}} | = 1\) nên \(|\overrightarrow {O{A_1}} | = \cos \alpha ,|\overrightarrow {O{A_2}} | = \cos \beta ,|\overrightarrow {O{A_3}} | = \cos \gamma \)
Ta có \(\overrightarrow {O{A_0}} = \overrightarrow {O{A_1}} + \overrightarrow {O{B_2}} + \overrightarrow {O{A_3}} \) , ta suy ra: \(\overrightarrow {O{A_0}} = \cos \alpha \overrightarrow i + \cos \beta \overrightarrow j + \cos \gamma \overrightarrow k \) hay \(\overrightarrow {O{A_0}} = (\cos \alpha ;\cos \beta ;\cos \gamma )\) .
Vì \(\overrightarrow {O{A_0}} = \overrightarrow {{a_0}} \) mà \(|\overrightarrow {{a_0}} | = 1\) nên ta có: \({\cos ^2}\alpha + {\cos ^2}\beta + {\cos ^2}\gamma = 1\)
Bài 3.10 trang 103 sách bài tập (SBT) – Hình học 12
Cho hình tứ diện ABCD.
a) Chứng minh hệ thức:
\(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)
b) Từ hệ thức trên hãy suy ra định lí: “Nếu một hình tứ diện có hai cặp cạnh đối diện vuông góc với nhau thì cặp cạnh đối diện thứ ba cũng vuông góc với nhau.”
Hướng dẫn làm bài:
a) Ta có
\(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} (\overrightarrow {AD} - \overrightarrow {AC} ) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \) (1)
\(\overrightarrow {AC} .\overrightarrow {DB} = \overrightarrow {AC} (\overrightarrow {AB} - \overrightarrow {AD} ) = \overrightarrow {AC} .\overrightarrow {AB} - \overrightarrow {AC} .\overrightarrow {AD} \) (2)
\(\overrightarrow {AD} .\overrightarrow {BC} = \overrightarrow {AD} (\overrightarrow {AC} - \overrightarrow {AB} ) = \overrightarrow {AD} .\overrightarrow {AC} - \overrightarrow {AD} .\overrightarrow {AB} \) (3)
Lấy (1) + (2) + (3) ta có hệ thức cần chứng minh là:
\(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\)
b) Từ hệ thức trên ta suy ra định lí: “Nếu tứ diện ABCD có \(AB \bot CD,AC \bot DB\) , nghĩa là \(\overrightarrow {AB} .\overrightarrow {CD} = 0\) và \(\overrightarrow {AC} .\overrightarrow {DB} = 0\) thì \(\overrightarrow {AD} .\overrightarrow {BC} = 0\) và do đó \(AD \bot BC\) .”
Bài 3.11 trang 103 sách bài tập (SBT) – Hình học 12
Tính tích vô hướng của hai vecto \(\overrightarrow a ,\overrightarrow b \) trong không gian với các tọa độ đã cho là:
a) \(\overrightarrow a = (3;0; - 6),\overrightarrow b = (2; - 4;c)\)
b) \(\overrightarrow a = (1; - 5;2),\overrightarrow b = (4;3; - 5)\)
c) \(\overrightarrow a = (0;\sqrt 2 ;\sqrt 3 ),\overrightarrow b = (1;\sqrt 3 ; - \sqrt 2 )\)
Hướng dẫn làm bài
a) \(\overrightarrow a .\overrightarrow b = 6(1 - c)\) ;
b) \(\overrightarrow a .\overrightarrow b = - 21\)
c) \(\overrightarrow a .\overrightarrow b = 0\)
Bài 3.12 trang 103 sách bài tập (SBT) – Hình học 12
Tính khoảng cách giữa hai điểm A và B trong mỗi trường hợp sau:
a) A(4; -1; 1) , B(2; 1; 0)
b) A(2; 3; 4) , B(6; 0; 4)
Hướng dẫn làm bài
a) \(|\overrightarrow {AB} | = 3\)
b) \(|\overrightarrow {AB} | = 5\)
congdong.edu.vn