Lớp 12 - SBT Toán học Giải bài 3.5, 3.6, 3.7, 3.8 trang 102 Sách bài tập Hình học 12
Bài 3.5 trang 102 sách bài tập (SBT) – Hình học 12
Trong không gian Oxyz, hãy tìm trên mặt phẳng (Oxz) một điểm M cách đều ba điểm A(1; 1; 1), B(-1; 1; 0), C(3; 1; -1).
Hướng dẫn làm bài:
Điểm M thuộc mặt phẳng (Oxz) có tọa độ là (x; 0; z), cần phải tìm x và z. Ta có:
MA2 = (1 – x)2 + 1 + (1 – z)2
MB2 = (–1 – x)2 + 1 + z2
MC2 = (3 – x)2 + 1 + (–1 – z)2
Theo giả thiết M cách đều ba điểm A, B, C nên ta có MA2 = MB2 = MC2
Từ đó ta tính được M(56;0;−76)
Bài 3.6 trang 102 sách bài tập (SBT) – Hình học 12
Cho hình tứ diện ABCD. Chứng minh rằng:
a) →AC+→BD=→AD+¯BC
b)→AB=12→AC+12→AD+12→CD+→DB
Hướng dẫn làm bài:
a) Ta có: →AC=→AD+→DC
→BD=→BC+→CD
Do đó: →AC+→BD=→AD+→BC vì →DC=−→CD
b) Vì →AB=→AD+→DB và →AD=→AC+→CD nên →AB=→AC+→CD+→DB
Do đó: 2→AB=→AC+→AD+→CD+2→DB
Vậy →AB=12→AC+12→AD+12→CD+→DB
Bài 3.7 trang 102 sách bài tập (SBT) – Hình học 12
Cho hình tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AC, BD, AD, BC. Chứng minh rằng:
a) →AB+→CD=→AD+→CB=2→MN
b) →AB−→CD=→AC−→BD=2→PQ
Hướng dẫn làm bài:
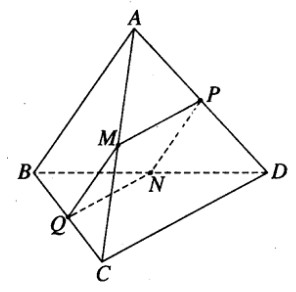
a) Ta có MPNQ là hình bình hành vì →MP=→QN=12→CD và →MQ=→PN=12→AB.
Do đó →MN=→MQ+→MP=→AB2+→CD2 hay 2→MN=→AB+→CD (1)
Mặt khác →AB=→AD+→DB
→CD=→CB+→BD
Nên →AB+→CD=→AD+→CB (2)
Vì →DB=−→BD
Từ (1) và (2) ta có: →AB+→CD=→AD+→CB=2→MN là đẳng thức cần chứng minh.
b) Ta có: →PQ=→MQ−→MP=→AB2−→CD2
Do đó: 2→PQ=→AB−→CD (3)
Mặt khác: →AB=→AC+→CB
→CD=→BD−→BC
Nên →AB−→CD=→AC−→BD (4)
Vì →CB−(−→BC)=→0
Từ (3) và (4) ta suy ra →AB−→CD=→AC−→BD=2→PQ là đẳng thức cần chứng minh.
Bài 3.8 trang 102 sách bài tập (SBT) – Hình học 12
Trong không gian cho ba vecto tùy ý →a,→b,→c . Gọi →u=→a−2→b,→v=3→b−→c,→w=2→c−3→a .
Chứng tỏ rằng ba vecto →u,→v,→w đồng phẳng.
Hướng dẫn làm bài:
Muốn chứng tỏ rằng ba vecto →u,→v,→w đồng phẳng ta cần tìm hai số thực p và q sao cho →w=p→u+q→v.
Giả sử có →w=p→u+q→v
2→c−3→a=p(→a−2→b)+q(3→b−→c)
⇔(3+p)→a+(3q−2p)→b−(q+2)→c=→0 (1)
Vì ba vecto lấy tùy ý →a,→b,→c nên đẳng thức (1) xảy ra khi và chỉ khi:
{3+p=03q−2p=0q+2=0⇒{p=−3q=−2
Như vậy ta có: →w=−3→u−2→v nên ba vecto →u,→v,→w đồng phẳng.
congdong.edu.vn