Lớp 12 - SBT Toán học Giải bài 2.6, 2.7, 2.8 trang 102, 103 Sách bài tập Giải tích 12
Bài 2.6 trang 102 Sách bài tập (SBT) Giải tích 12
Tìm tập xác định của các hàm số sau:
a) \(y = {({x^2} - 4x + 3)^{ - 2}}\)
b) \(y = {({x^3} - 8)^{{\pi \over 3}}}\)
c) \(y = {({x^3} - 3{x^2} + 2x)^{{1 \over 4}}}\)
d) \(y = {({x^2} + x - 6)^{ - {1 \over 3}}}\)
Hướng dẫn làm bài:
a) Hàm số xác định khi \({x^2} - 4x + 3 \ne 0\) hay \(x \ne 1;x \ne 3\).
Vậy tập xác định của hàm số đã cho là R\{1; 3}.
b) Hàm số xác định khi x3 – 8 > 0 hay x > 2. Vậy tập xác định là \((2; + \infty )\) .
c) Hàm số xác định khi x3 – 3x2 + 2x > 0 hay x(x – 1)(x – 2) > 0
Suy ra 0 < x < 1 hoặc x > 2. Vậy tập xác định là \((0;1) \cup (2; + \infty )\)
d) Hàm số xác định khi x2 + x – 6 > 0 hay x < -3 và x > 2.
Vậy tập xác định là \(( - \infty ; - 3) \cup (2; + \infty )\).
Bài 2.7 trang 103 Sách bài tập (SBT) Giải tích 12
Tính đạo hàm của các hàm số cho ở bài 2.6
a) \(y = {({x^2} - 4x + 3)^{ - 2}}\)
b) \(y = {({x^3} - 8)^{{\pi \over 3}}}\)
c) \(y = {({x^3} - 3{x^2} + 2x)^{{1 \over 4}}}\)
d) \(y = {({x^2} + x - 6)^{ - {1 \over 3}}}\)
Hướng dẫn làm bài:
a) \(y' = - 2{({x^2} - 4x + 3)^{ - 3}}(2x - 4)\)
b) \(y' = {\pi \over 3}{({x^3} - 8)^{{\pi \over 3} - 1}}.3{x^2} = \pi {x^2}{({x^3} - 8)^{{\pi \over 3} - 1}}\)
c) \(y' = {1 \over 4}{({x^3} - 3{x^2} + 2x)^{ - {3 \over 4}}}(3{x^2} - 6x + 2)\)
d) \(y' = - {1 \over 3}{({x^2} + x - 6)^{ - {4 \over 3}}}(2x + 1)\).
Bài 2.8 trang 103 Sách bài tập (SBT) Giải tích 12
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:
a) \(y = {x^{ - 3}}\)
b) \(y = {x^{ - {1 \over 2}}}\)
c) \(y = {x^{{\pi \over 4}}}\)
Hướng dẫn làm bài:
a) Tập xác định: R\{0}
Hàm số đã cho là hàm số lẻ.
\(y' = - 3{x^{ - 4}} = - {3 \over {{x^4}}}\)
Ta có: \(y' < 0,\forall x \in R\backslash {\rm{\{ }}0\}\) nên hàm số luôn nghịch biến trên các khoảng xác định.
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to + \infty } y = 0,\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to {0^ - }} y = - \infty \)
Đồ thị có tiệm cận ngang là trục hoành, tiệm cận đứng là trục tung.
Bảng biến thiên:
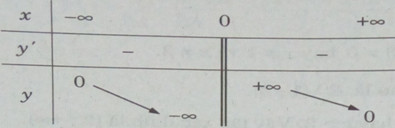
Đồ thị của hàm số có tâm đối xứng là gốc tọa độ.
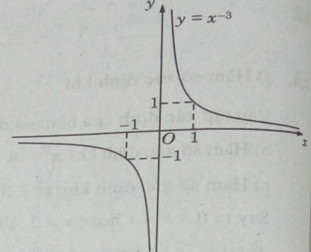
b) Tập xác định: \(D = (0; + \infty )\)
\(y' = - {1 \over 2}{x^{ - {3 \over 2}}}\)
Vì nên hàm số nghịch biến.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = + \infty ,\mathop {\lim }\limits_{x \to + \infty } y = 0\)
Đồ thị có tiệm cận đứng là trục tung, tiệm cận ngang là trục hoành.
Bảng biến thiên:
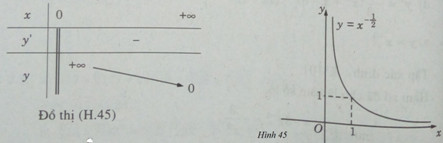
c) Tập xác định: \(D = (0; + \infty )\)
\(y' > 0,\forall x \in D\)
Vì \(y' > 0,\forall x \in D\) nên hàm số nghịch biến.
\(\mathop {\lim }\limits_{x \to {0^ + }} y = 0,\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
Đồ thị không có tiệm cận.
Bảng biến thiên
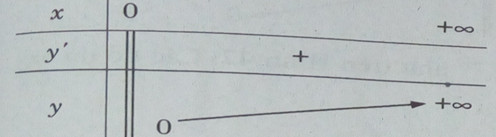
Đồ thị
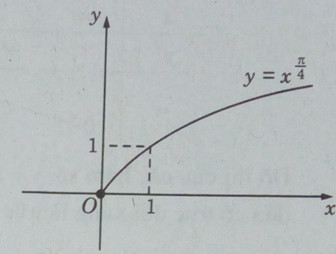
congdong,\.edu.vn